This article, written by the Facebook research team, was written by Ben Letham, Brian Karrer, Guilherme Ottoni and Eytan Bakshy. It features some of the techniques used by Facebook for A/B testing.
Facebook relies on a large suite of backend systems to serve billions of people each day. Many of these systems have a large number of internal parameters. For example, the web servers that power Facebook use the HipHop Virtual Machine (HHVM) to serve requests, and HHVM has dozens of parameters that control the just-in-time compiler. As another example, machine learning systems are used for a variety of prediction tasks. These systems typically involve multiple layers of predictive models, with a large number of parameters for determining how the models are linked together to yield a final recommendation. Such parameters must be carefully tuned through the use of live, randomized experiments, otherwise known as A/B tests. Each of these experiments may take a week or longer, and so the challenge is to optimize a set of parameters with as few experiments as possible.
A/B tests are often used as one-shot experiments for improving a product. In our paper Constrained Bayesian Optimization with Noisy Experiments, now in press at the journal Bayesian Analysis, we describe how we use an AI technique called Bayesian optimization to adaptively design rounds of A/B tests based on the results of prior tests. Compared to a grid search or manual tuning, Bayesian optimization allows us to jointly tune more parameters with fewer experiments and find better values. We have used these techniques for dozens of parameter tuning experiments across a range of backend systems, and have found that it is especially effective at tuning machine learning systems.
Bayesian optimization for A/B testing
A typical approach for tuning parameters of an online system is to manually run small grid searches to optimize each parameter separately. Bayesian optimization constructs a statistical model of the relationship between the parameters and the online outcomes of interest, and uses that model to decide which experiments to run. This model-based approach has several key advantages, especially for tuning online machine learning systems.
Better scaling with parameter dimensionality: Given the limitations on the number of online experiments that can be run, grid search or manual tuning cannot be used to tune more than a couple parameters simultaneously. The use of models allows Bayesian optimization to scale to a much larger number of parameters; we routinely optimize up to 20 parameters jointly. This is important for machine learning systems where there are frequently interactions between parameters that necessitate joint optimization.
Reduced number of experiments: Bayesian optimization allows us to borrow strength across rounds of experimentation: A test of a parameter value in a continuous space gives us information about not only its outcome, but also those of nearby points. This allows us to greatly reduce the number of experiments needed to explore the space.
Better experiment outcomes: The model is able to identify parts of the space that are unlikely to provide a good outcome, and avoid running tests of those parameter values. This improves the experience inside the treatment groups.
Understand the parameter space: Modeling allows us to visualize and better understand how the parameters affect the outcome of interest.
We now provide a high-level description of Bayesian optimization, and then describe the work from the paper and some of the experimental results given there.
Bayesian optimization
Bayesian optimization is a technique for solving optimization problems where the objective function (i.e., the online metric of interest) does not have an analytic expression, rather it can only be evaluated through some time consuming operation (i.e., a randomized experiment). The key to efficiently exploring a multidimensional space with a limited number of experiments is modeling: The true objective function is unknown, but we can fit a model to the observations we have so far and use the model to predict good parts of the parameter space where we should run additional experiments.
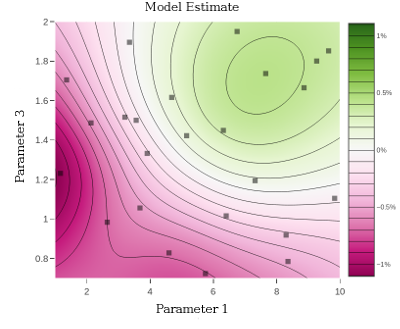
The Gaussian process (GP) is a nonparametric Bayesian model that works well for Bayesian optimization because it provides excellent uncertainty estimates and is analytically tractable.
Each data marker in the figure above corresponds to the outcome of an A/B test of that parameter value. We can use the GP to decide which parameter to test next by balancing exploration (high uncertainty) with exploitation (good model estimate). This is done by computing an acquisition function that estimates the value of running an experiment with any given parameter value.
To read the whole article, with formulas and illustrations, click here.
DSC Resources
- Free Book and Resources for DSC Members
- New Perspectives on Statistical Distributions and Deep Learning
- Time series, Growth Modeling and Data Science Wizardy
- Statistical Concepts Explained in Simple English
- Machine Learning Concepts Explained in One Picture
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- How to Automatically Determine the Number of Clusters in your Data
- Fascinating New Results in the Theory of Randomness
- Hire a Data Scientist | Search DSC | Find a Job
- Post a Blog | Forum Questions