
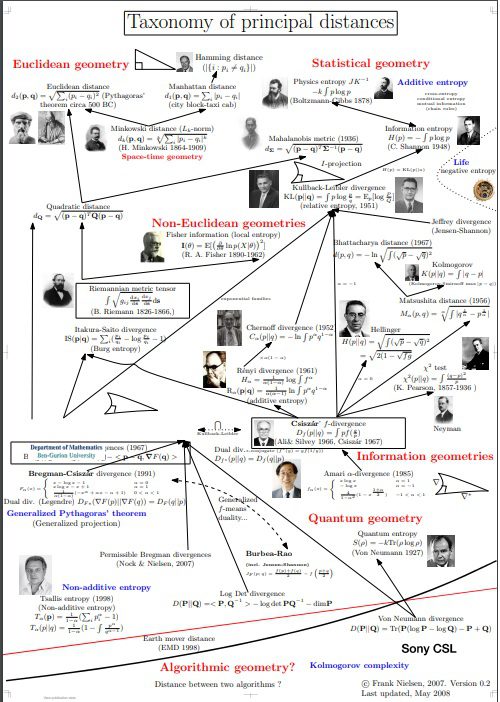
I saw a nice representation of distance metrics.
This topic is not easy to explain.
This representation provides a good overview (link below to download larger pdf image)
In statistics, probability theory, and information theory, a statistical distance quantifies the distance between two statistical objects, which can be two random variables, or two probability distributions or samples, or the distance can be between an individual sample point and a population or a wider sample of points. (source wikipedia)
The concept of statistical distance is also related to that of probabilistic metric spaces where the distances between points are specified by probability distributions rather than numbers. Distances and similarities are measures to describe how close two statistical objects are. Depending on the problem at hand, multiple distances could apply between two points. For example, Euclidean distance and the linear correlation coefficient can represent the distance and similarity measures respectively between the same two points. Similarly, the Mahalanobis distance can be used for outlier detection. .
Common statistical measure include
• Population Stability Index (PSI)
• Kullback–Leibler divergence (KL-Divergence)
• Jensen–Shannon divergence (JS-Divergence)
• Earth Mover’s Distance (EMD)
They have a variety of applications depending on industry.
PSI: is used in the finance industry. PSI is used as a distribution check to detect changes in the distributions that might make a feature less valid as an input to the model. It is used often in finance to monitor input variables into models.
KL Divergence: The KL divergence is useful if one distribution has a high variance relative to another or small sample size. KL Divergence is a well-known metric that can be thought of as the relative entropy between a sample distribution and a reference (prior) distribution.
We see how this idea can apply to quantum problems:
Statistical distance and the geometry of quantum states is a well-referenced paper that says:
By finding measurements that optimally resolve neighboring quantum states, we use statistical distinguishability to define a natural Riemannian metric on the space of quantum-mechanical density operators and to formulate uncertainty principles that are more general and more stringent than standard uncertainty principles.
So, to conclude, these ideas are worth knowing and have wide applicability
The image lists types of distances including:
- Euclidian
- Statistical
- Non-Euclidian
- Informational and
- Quantum
Image source: (you can download a larger pdf file)
https://www.researchgate.net/publication/329060274_Taxonomy_of_principal_distances
References
Using statistical distance metrics for machine learning observability
