More Math Hallucinations with OpenAI, worse with Gemini

This is not just another rant about OpenAI. I actually have something very positive to say, even if in the end, the answer to my prompt was wrong. It started with the following question: What is the length of the period of 1/10! in base 2 (the binary system)? Here the exclamation point denotes the factorial. For instance, 5! = 5 x 4 x 3 x 2 x 1. Satellite prompts included “the full period” rather than just the length, the proportion of zeros and ones in the full period, and the length of the period of 1/n!

All in base 2, that is, in the binary number system. I explain at the bottom of this article why I am interested in this problem. In my opinion, that’s the most interesting part. For the reader to understand the remaining, I now need to introduce two basic concepts: the prefix and period of a fraction.

Every rational number can be written as a sequence of digits. For instance, in base 10 (decimal system):

\frac{1213}{2775}=0.43711711711711711\dots

In this example, the period is 711 and its length is 3 (we have 3 repeating digits). The prefix, here 43, is the beginning before the periodic sequence kicks in. In the binary system, digits are either 0 or 1.

First Try with OpenAI

I first tried to find the length of the period for 1/10! As you can see in Figure 1, OpenAI found something clearly related to my prompt. It took around 10 seconds to generate the full answer, doing computations on the fly. In the end, it came with 12 for the length of the period in base 2. The correct answer is 540. I did not have the time to investigate what is wrong in OpenAI computations. At least, I knew it was wrong! If you don’t, you may end up doing research, publish articles, design systems, or make recommendations that are faulty.

Note that when asked for the period length for 1/n! OpenAI is able to generalize and will show the process for an arbitrary integer n, using the same method. It would be nice if it could provide a reference, but it does not.

Second Try with OpenAI

To investigate the issue, I asked for the full period, not just its length. Here something interesting happened. OpenAI retrieved some Python code — see Figure 2 — and executed it on the fly.

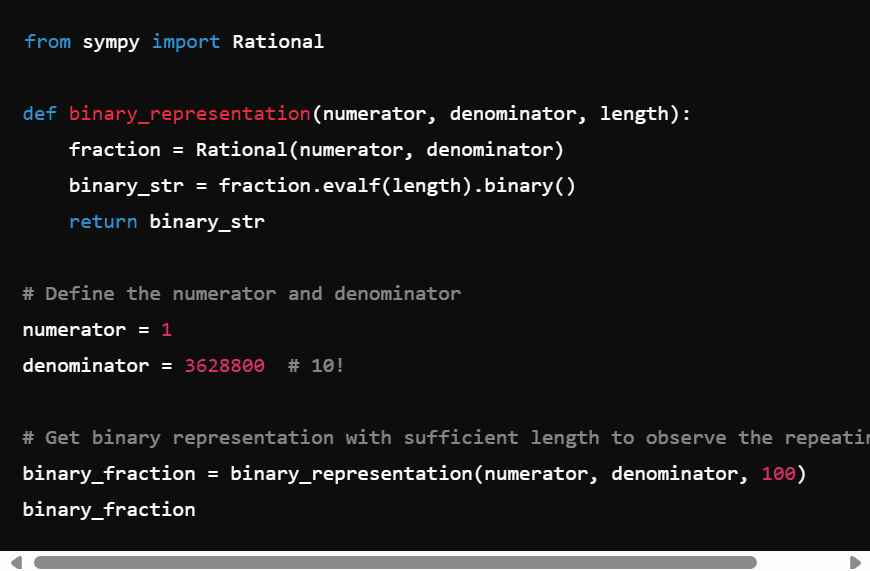
Then, the results were displayed on my screen. That is, the first 100 binary digits of 1/10! including the prefix. Not shown here because the beginning consists of zeros only. Surprisingly, a few days earlier, via a Google search, I had found the same Python code. It took me about 10 minutes to find it on Google, much more time than on OpenAI because I had to try many queries. The code found on Google was for decimal numbers, not binary. Nevertheless, with slight changes, it worked for binary numbers, returning the correct answer.

So, at this point, I can say that OpenAI succeeded. Even better: it showed me that the function in question (“binary representation”) is part of the SymPy library, a symbolic math library that I didn’t know existed in Python. For me, it was the culmination, a great value, more than I had expected, because now I can explore all the other functions in that library.

But from there, it went downhill. I tested the function in question before, outside the SymPy environment, and I know that for 1/10! the length of the period is 540. Yet OpenAI finished its answer with the following conclusion:

To identify the repeating part, we need to examine this binary fraction closely. Given the sequence is quite long and not immediately showing repetition within the first 100 digits, we need to extend our calculation to capture more digits or use a more advanced method to pinpoint the repeating sequence.

However, manually or computationally, for accurate determination of the full repeating period, we generally rely on finding the LCM of the orders of 2 with respect to the prime factors other than 2 in the denominator. As calculated earlier, the period length is 12.

So, despite having found the correct answer for the full period using the Python code, OpenAI still maintained that the length of the period is 12 (wrong answer). Go figure…

Blending Results from Multiple Platforms

After this experiment, I came up with a new idea. Creating an app that would automatically crawl multiple GPTs: prompt results from OpenAI, Claude, Mistral, Gemini, and so on, using billions of generated prompts, distilling the results, and serving the best of the mix to the user. Not just for my query, but for all prompts (at least computer science related). In short, a meta-LLM based on multiple platforms.

The idea is particularly appealing to me since I designed my own LLM, known as xLLM: see here. Indeed, I found OpenAI prompt results to be a good source of augmented data, to blend with my own internal embeddings. Perhaps a future project for me or someone else. The idea received a lot of positive interest when I discussed it with other professionals. Now, if you are curious, here is Gemini’s meaningless answer to my original prompt:

[..] Therefore, 1/10! in binary would not have a repeating period. It would likely be a non-terminating binary number with a specific pattern of 0s and 1s that doesn’t necessarily repeat.

Addendum

I also tried another prompt: count the number of occurrences of “000” in all binary strings of length 5. Then, same prompt with “000” replaced by “010”. OpenAI claims the answer is 8 in both cases. Gemini claims it is 3. Both justify the wrong answer using incorrect logic. Even Python gets it wrong, counting non-overlapping occurrences only, coming up with 8 for “000” (wrong) and 11 for “010” (correct).

Why am I Interested in those Digits?  

Almost nothing is known about the digit distribution of any classic mathematical constant such as π, e, log 2, the square root of 2, or any combination of these. This is true regardless of the base system: decimal, binary or other. For instance, in the binary system, no one knows the proportion of zeros and ones for any of these numbers.

Indeed, this is one of the most difficult mathematical problems of all times, arguably even more challenging than the Riemann Hypothesis, also unsolved. The only established fact is that the digits do not repeat: the period is infinite. Also, for any random number, the digit distribution is even. Exceptions are incredibly rare, though it encompasses infinitely many rational numbers, for instance the one mentioned in the introduction. All the famous math constants pass all the statistical tests of randomness for the first few trillions of digits. They are believed to have an even (uniform) digit distribution. But there is no proof. Nothing even remotely close.

Towards a Seminal Result on the Digits of e

In order to make progress on this problem, I came up with a new framework. First, for any strictly positive integers n, m, z, I define the fraction p_n(z, m)/q_n(z, m) using the recursion

\begin{align}
 p_{n} = &  z\cdot (1 + \bmod_mn ) \cdot p_{n-1} + 1\\
q_{n} = & z\cdot (1+\bmod_mn) \cdot q_{n-1}
\end{align}

with p₁(z, m) = 0 and q₁(z, m) = z. Here mod_m n stands for n modulo m. When m is finite, all these fractions represent rational numbers even when n is infinite. Thus, studying their digit distributions should be less challenging. It involves very fast computation of p-adic valuations. It also comes with nice convergence properties when n or m (or both) tend to infinity.

When both m and n are infinite, the fraction represents one of the famous irrational math constants. That’s the first key to solving the problem. If I succeed — if I prove any spectacular result regarding the digit distribution of the constant in question — I will publish it in a paper entitled “Some Properties of the Long Division Algorithm Taught in Elementary School”.

You might ask: What is the connection to the period of 1/n!

If m is infinite and z = 1, then q_n(z, m) = n! However, studying the period of n! leads to nowhere but fallacious proofs. The second key to correctly proving the infamous conjecture, is to focus on the prefix, not the period. The prefix, that is, the first few digits before the period starts, grows very slowly in length as n tends to infinity. This is in sharp contrast to the period behavior. Yet, the length of the prefix eventually becomes infinite, matching all the digits of the irrational math constant in question. You should completely ignore the period and focus on the prefix instead. In base b, you can compute the prefix at iteration n with the formula

\text{Prefix} = \Big\lfloor \frac{b^{v_b(q_n)} \cdot p_n}{q_n}\Big\rfloor,

where the brackets represent the floor function, and v_b(q_n) is the p-adic valuation of q_n in base b: that is, the exponent attached to the largest power of b that divides q_n.

The next step is to explore different bases, not just the binary system. Unfortunately, for now, my framework works only if the base is a prime number: 2, 3, 5, 7, 11 and so on, but not 10 (the decimal system). Finally, the short summary outlined here is just the tip of the iceberg. There is a lot more already in place. Note that p_n(z, m) is a polynomial in z, of degree n, with integer coefficients. Even when m is infinite.

About the Author

Vincent Granville is a pioneering GenAI scientist and machine learning expert, co-founder of Data Science Central (acquired by a publicly traded company in 2020), Chief AI Scientist at MLTechniques.com and GenAItechLab.com, former VC-funded executive, author (Elsevier) and patent owner — one related to LLM. Vincent’s past corporate experience includes Visa, Wells Fargo, eBay, NBC, Microsoft, and CNET. Follow Vincent on LinkedIn.