New & Notable
Top Webinar
DSC Webinar Series: How to Scale NiFi Deployments to Enable Universal Data Distribution
Ben Cole | August 29, 2023 at 3:08 pmRecently Added
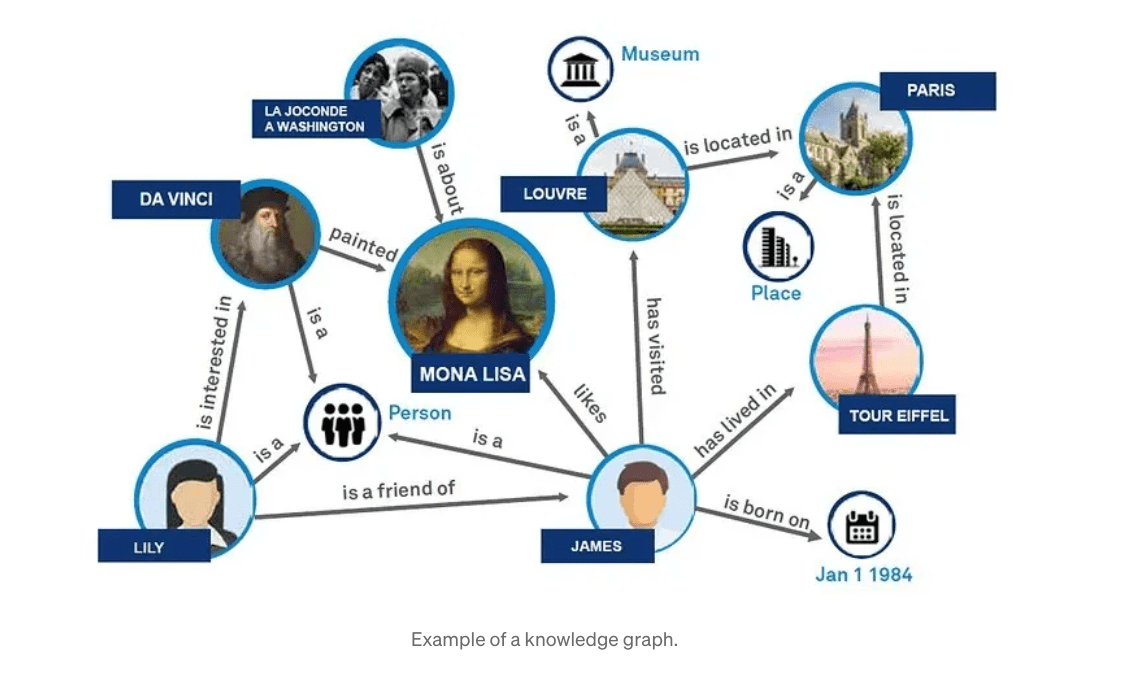
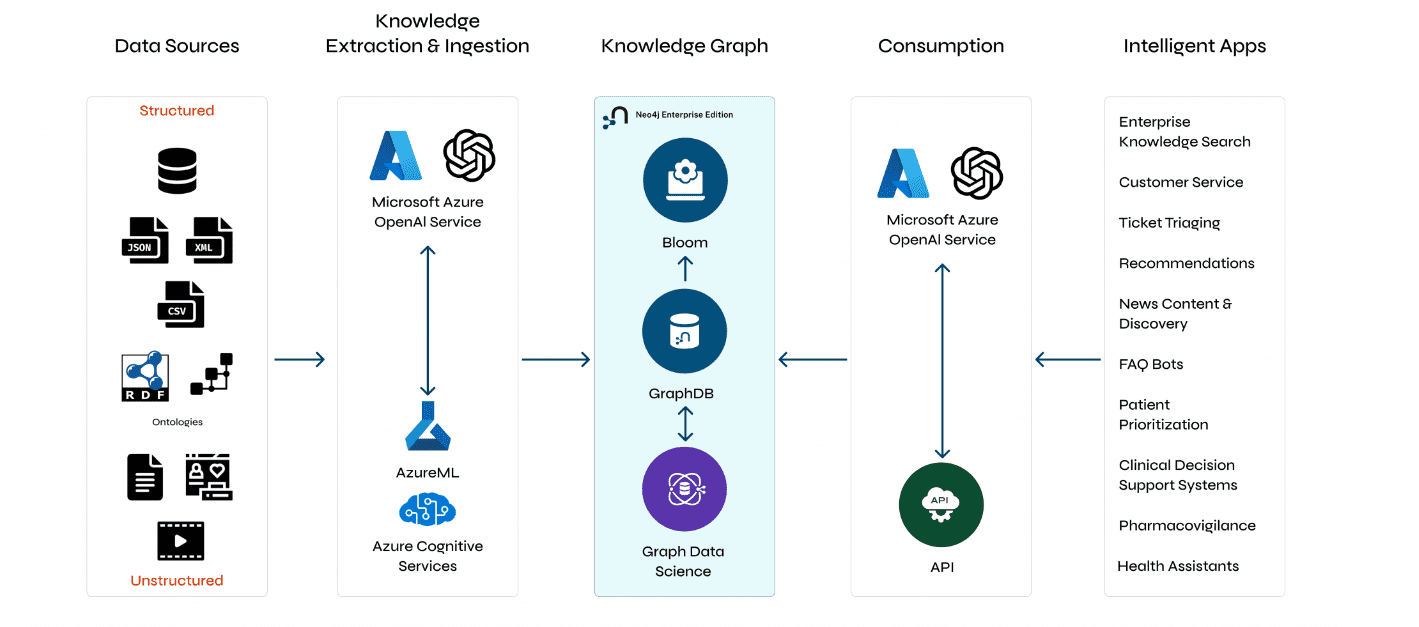
Understanding GraphRAG – 1: The challenges of RAG
ajitjaokar | April 26, 2024 at 1:45 pmBackground Retrieval Augmented Generation(RAG) is an approach for enhancing existing LLMs with external knowledge source...
Optimizing model training: Strategies and challenges in artificial intelligence
Pritesh Patel | April 25, 2024 at 2:51 pmWhen you do model training, you send data through the network multiple times. Think of it like wanting to become the bes...
Top AI Influencers to Follow in 2024
Vincent Granville | April 25, 2024 at 1:28 amThere are many ways to define “top influencer”. You may just ask OpenAI to get a list: see results in Figure...
Losing control of your company’s data? You’re not alone
Alan Morrison | April 24, 2024 at 1:10 pmPhoto by Hermann Traub on Pixabay Losing control of your company’s data? You’re not alone To survive and thr...
DSC Weekly 23 April 2024
Scott Thompson | April 23, 2024 at 2:29 pmAnnouncements Top Stories In-Depth...
How to implement big data for your company
Yana Ihnatchyck | April 23, 2024 at 10:50 amBig data analytics empowers organizations to get valuable insights from vast and intricate data sets, offering a pathway...
Understanding GraphRAG – 2 addressing the limitations of RAG
ajitjaokar | April 22, 2024 at 4:08 pmBackground We follow on from the last post and explore the limitations of RAG and how you can overcome these limitations...
How predictive analytics improves payment fraud detection
Zachary Amos | April 22, 2024 at 3:09 pmPayment fraud is a significant issue for banks, customers, government agencies and others. However, advanced predictive ...
Understanding GraphRAG – 3 Implementing a GraphRAG solution
ajitjaokar | April 22, 2024 at 10:59 amIn this third part of the solution, we discuss how to implement a GraphRAG. This implementation needs an understanding o...
Quantization and LLMs – Condensing models to manageable sizes
Kevin Vu | April 19, 2024 at 3:39 pmThe scale and complexity of LLMs The incredible abilities of LLMs are powered by their vast neural networks which are ma...
New Videos
Implementing AI in K-12 education
Roundtable Discussion with Rebecca Bultsma and Ahmad Jawad In the latest episode of the AI Think Tank Podcast, we ventured into the rapidly evolving intersection…
Retrieval augmented fine-tuning and data integrations
Presentation and discussion with Suman Aluru and Caleb Stevens In the latest episode of the “AI Think Tank Podcast,” I had the pleasure of hosting…
7 GenAI & ML Concepts Explained in 1-Min Data Videos
Not your typical videos: it’s not someone talking, it’s the data itself that “talks”. More precisely, data animations that serve as 60-seconds tutorials. I selected…