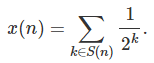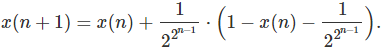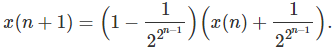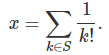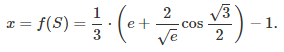Here are a few off-the-beaten-path problems at the intersection of computer science (algorithms), probability, statistical science, set theory, and number theory. While they can easily be understood by beginners, finding a full solution to some of them is not easy, and some of the simple but deep questions below won’t be answered for a long time, if ever, even by the best mathematicians living today. In some sense, this is the opposite of classroom exercises, as there is no sure path that leads to full solutions. I offer partial solutions and directions, to help solve these problems.
Mathematical tessellation artwork
1. A Special Number
Here we try to construct an irrational number x that has 50% of zero’s, and 50% of one’s, in its binary representation (digits in base 2.) To this day, no one knows whether any classic mathematical constant (Pi, e, log 2, SQRT(2) and so on) has such a uniform distribution of 0 and 1 in base 2, or any other base. The number is constructed as follows. Let us denote as S(n) the set of strictly positive integers that are divisible by p(1) or p(2) or … or p(n) where the p(k)’s are prime numbers to be determined later. We formally define x as the limit, when n tends to infinity, of x(n), with
The prime numbers p(1), p(2) and so on, are chosen such that x has 50% zero’s, and 50% one’s, in its base 2 representation. Which prime numbers we should choose is a relatively easy problem, achieved using a version of the greedy algorithm as follows:
- p(1) can not be 2 (why?) and the smallest value it can possibly be is p(1) = 3. Let’s pick p(1) = 3. Now, one third of the digits of x(1) are equal to 1.
- p(2) = 5 works. So let’s pick p(2) = 5. Now the proportion of 1 in the digits of x(2), is 7/15 still lower than 50%.
- p(3) = 7 does not work because x(3) — and thus x(4), x(5), x(6) and so on — would have more than 50% of its digits equal to 1. The smallest prime to choose next is p(3) = 17. With this choice, the proportion of 1 in the digits of x(3), is 0.498039216.
- The smallest next prime that works, is p(4) = 257. With this choice, the proportion of 1 in the digits of x(4), is 0.49999237.
Now we have an algorithm to find the p(k)’s. It is easy to prove (see here) that the proportion of 1 in x(n), denoted as r(n), is equal to
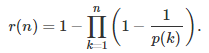
Note that this formula is correct only if the p(k)’s have no common divisors (why?), thus our focus is on prime numbers only. The fact that the above product, if taken over all prime numbers rather than those few that we picked, is diverging, actually guarantees that we can grow our list of primes indefinitely, and at the limit as n tends to infinity, have r(n) tends to 50%, as desired. In short, prime numbers are abundant enough for this to work, while squares of prime numbers would be too few for this to work (the above product, if taken over all squares of prime numbers, converges, causing the problem). Also note that for any fixed value of n, x(n) is a rational number and can be computed explicitly.
Questions
- Can you find the first 10 values of p(n)? What about the first 50 values? (you will need high precision computing for that)
- Is the number x constructed here, rational or not?
- Compute the first 10 decimals (in base 10) of x.
- Compute the exact values of x(n) up to n = 5.
- Provide an asymptotic formula for p(n) — this article might help you find the answer. In short, p(n+1) is of the same order of magnitude as the square of p(n).
- Is the digit distribution of x truly random?
The answer to the last question is no. The digits exhibit strong auto-correlations, by construction. It is also easy to prove that x is not a normal number, since sequences of digits such as “100001” never appear in its base 2 representation.
2. Another Special Number
Again, the purpose here is to construct an irrational number x between 0 and 1, with the same proportion of digits equal either to 1 or 0, in base 2. I could call it the infinite mirror number, and it is built as follows, using some kind of mirror principle:
- The first digit is 0.
- First 2 digits: 0 | 1
- First 4 digits: 0, 1 | 1, 0
- First 8 digits: 0, 1, 1, 0 | 1, 0, 0, 1
- First 16 digits: 0, 1, 1, 0, 1, 0, 0, 1 | 1, 0, 0, 1, 0, 1, 1, 0
- And so on.
Can you guess the pattern? Solution: at each iteration, concatenate two strings of digits: the one from the previous iteration, together with the one from the previous iteration with 1 replaced by 0 and 0 replaced by 1. This leads to the following recursion, starting with x(1) = 0:
That is,
The number x, defined as the limit of x(n) as n tends to infinity, share a few properties with the number discussed in the first problem:
- x(n) is always a rational number, easy to compute exactly.
- The proportion of digits of x, equal to 0 in base 2, is 50% by construction.
- The number x is not normal: the sequence of digits “111” never appears in its binary expansion.
Is x is a rational number? I could not find any period in the first few hundred digits of x in base 2; it makes me think that this number is probably irrational. Can you compute the first 10 decimals of x, in base 10?
Finally, the digit 0 (in base 2) appears in the following positions:
1, 4, 6, 7, 10, 11, 13, 16, 18, 19, 21, 24, 25, 28, 30, 31, 34, 35, 37, 40, 41, 44, 46, 47, 49, 52, 54, 55, 58, 59, 61, 64, 66, 67, 69, 72, 73, 76, 78, 79, 81, 84, 86, 87, 90, 91, 93, 96, 97, 100, 102, 103, 106, 107, 109, 112, 114, 115, 117, 120, 121, 124, 126, 127, …
Do you see any patterns in that sequence?
Another number with digits uniformly distributed, although in base 10, is the Champernowne constant, defined as 0.12345678910111213… That number is even normal. Yet unlike Pi or SQRT(2), it fails many tests of randomness, see the section “failing the gap test” in chapter 4 in my book. Rather than using the concept of normal number, a better definition of a number with “random digits” is to use my concept of “good seed” (discussed in the same book) which takes into account the joint distribution of all the digits, not just some marginals. Note that for some numbers, the distribution of the digits does not even exist. See chapter 10 in the same book for an example.
Exercise
Analyze the digit distribution, in base 2, of the following numbers:
- The number that has it’s k-th digit in base 2, equal to 1 if and only if the fractional part of k * Pi is less than 0.5. This number should be irrational because Pi is irrational (right?) and the digit distribution uniform because of the equidistribution theorem.
- The number that has it’s k-th digit in base 2, equal to 1 if and only if the number of distinct prime factors of k is odd. Starting points to answer this question, are this link and this one. The proportion of integers with an odd number of distinct prime factors seems to be 1/2 as you would expect, but it looks like this result hasn’t been proved so far (so I suppose it must be a conjecture.) It seems that this proportion is always below 1/2 but nevertheless converging to 1/2 — see here for more details. I made a separate article about a generalization of this problem, see here.
Is there a number, say x, other than Pi, such that the fractional part of k * Pi is less than 0.5, if and only if the fractional part of k * x is less than 0.5, for all k?
3. Representing Sets by Numbers or Functions
Here we try to characterize a set of strictly positive integer numbers by a real number, or a set of real numbers by a function.
If S is a set of strictly positive integers, one might characterize S by the number f(S) = x, defined as follows: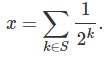 However, this approach has some drawbacks: for instance, f({1}) = f({2,3,4,5,6,…}) = 1/2. In short, all finite sets have a number representation that is also matched by an infinite set. How can we walk around this issue? If instead of using the representation using the base 2 system as above, we use the logistic map representation (see chapter 10 in my book), would this solve the issue? That is, in the logistic map numeration system, where digits are also equal to either 0 or 1, can two different sets be represented by the same number?
However, this approach has some drawbacks: for instance, f({1}) = f({2,3,4,5,6,…}) = 1/2. In short, all finite sets have a number representation that is also matched by an infinite set. How can we walk around this issue? If instead of using the representation using the base 2 system as above, we use the logistic map representation (see chapter 10 in my book), would this solve the issue? That is, in the logistic map numeration system, where digits are also equal to either 0 or 1, can two different sets be represented by the same number?
Let’s turn now to sets consisting of real numbers. But first, let’s mention that there is enough real numbers in [0, 1] to characterize all sets consisting only of integer numbers: in short, in principle, there is a one-to-one mapping between sets of integers, and real numbers. Unfortunately, there isn’t enough real numbers to characterize all sets of real numbers, thus we can not uniquely characterize a set of real numbers, by a real number. However there is enough real-valued functions to characterize all of them uniquely. See this article for an introduction on the subject.
The first idea that comes to my mind, to characterize a measurable bounded set S of real numbers, is to use the characteristic function of a uniform distribution on S. Two different sets will have two different characteristic functions, unless the difference between the two sets is a set of measure 0. It is not difficult to generalize this concept to unbounded sets, but how can you generalize it to non measurable sets? Also, many characteristic functions won’t represent a set; for instance, in this framework, no set can have the characteristic function of a Gaussian distribution. By contrast, for sets of strictly positive integer numbers, any real number in [0, 1] clearly represents a specific set. How to go around this issue?
Another interesting issue is to study how operations on sets (union, intersection, hyper-logarithm, and so on) look like when applied to the number or real-valued function that characterize them.
The next tricky question of course, is how to represent sets of real-valued functions, by a mathematical object. There are not enough characteristic functions, by far, to uniquely characterize these sets. Operators, a branch of functional analysis, might fit the bill. These are functions whose argument is a function itself, such as the integral or derivative operators. Finally, what kind of mathematical object should you use to uniquely characterize any set of mathematical operators? Obviously it will be some kind of mapping, let’s call it meta-operators, that have as argument, an operator. At this point, it is becoming extremely theoretical and abstract.
Exercise
Back to the problem of representing a set S of strictly positive integers, by a real number x = f(S). Consider the following representation:
What are the pluses and minuses over the solution proposed at the beginning of this section?
Answer: all sets have a unique number attached to them, but some numbers, for instance any number strictly between 1 and e-1, do not represent any set. Note that if for instance, you consider the set S of numbers that are multiple of 3, you get a beautiful result for x = f(S): see here for details. The result is
Related Articles
- One Trillion Random Digits
- Curious Mathematical Problem
- Another Off-the-beaten-path Data Science Problem
- Two More Math Problems: Continued Fractions, Nested Square Roots, D…
- Mathematical Olympiads for Undergrad Students
- Difficult Probability Problem: Distribution of Digits in Rogue Systems
- Little Stochastic Geometry Problem: Random Circles
- Paradox Regarding Random (Normal) Numbers
- Curious Mathematical Object: Hyperlogarithms
- 88 percent of all integers have a factor under 100
- Fractional Exponentials – Dataset to Benchmark Statistical Tests
- Two Beautiful Mathematical Results – Part 2
- Two Beautiful Mathematical Results
- Four Interesting Math Problems
- Number Theory: Nice Generalization of the Waring Conjecture
- Fascinating Chaotic Sequences with Cool Applications
- Representation of Numbers with Incredibly Fast Converging Fractions
- Yet Another Interesting Math Problem – The Collatz Conjecture
- Simple Proof of the Prime Number Theorem
- Factoring Massive Numbers: Machine Learning Approach
- Representation of Numbers as Infinite Products
- A Beautiful Probability Theorem
- Fascinating Facts and Conjectures about Primes and Other Special Nu…
- Three Original Math and Proba Challenges, with Tutorial
For related articles from the same author, click here or visit www.VincentGranville.com. Follow me on on LinkedIn, or visit my old web page here.
DSC Resources
- Invitation to Join Data Science Central
- Free Book: Applied Stochastic Processes
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Post a Blog | Forum Questions