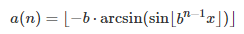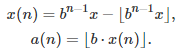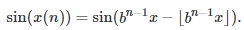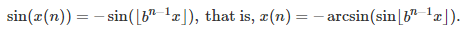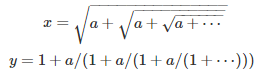Two More Math Problems: Continued Fractions, Nested Square Roots, Digits of Pi

These problems are for college undergrads after a first course in calculus. They are provided with solutions, and could be used by college professors as exercises or exam questions.

1. Digits of Pi/4

Prove that in base b, if b is an even integer, n > 3, and x = Pi/4, then the n-th digit of x, denoted as a(n), is given by the formula below. We start with n = 1 after the decimal point, for the first digit. Also show that the formula below is not valid if the base b is an odd integer, or if x is different from Pi/4.

where the brackets represent the integer part (also called floor) function.

Solution

Regardless of the number x in [0, 1] and the base b, the n-th digit a(n) of x can be computed as follows:

See here for details. Thus we have

Using the angle difference formula for sinus, the fact that n > 3, b is an even integer, and x = Pi/4, it simplifies to

The result for a(n) follows immediately.

2. Continued Fractions and Nested Square Roots

Let us consider the two following expressions, assuming a is a strictly positive real number:

Prove that x is an integer if and only if a is the product of two consecutive integers. Prove that the same is true for y.

Solution

Let’s focus on the first case. The second case is almost identical. The strictly positive number x must satisfy x^2 = a + x, thus x = (1 + SQRT(1 + 4a)) / 2. In order for x to be an integer, 1 + 4a must be a perfect odd square, which is possible only if a is the product of two consecutive integers. For instance,

If a = 1 * 2, then x = 2
If a = 2 * 3, then x = 3
If a = 3 * 4, then x = 4
If a = 4 * 5, then x = 5
and so on.

Note that the expansion of the number x = 2 in the nested square root numeration system, when x tends to 2, has all its “digits” equal to a = 1 * 2. See this spreadsheet for details. More on this here.

For related articles from the same author, click here or visit www.VincentGranville.com. Follow me on on LinkedIn.

Related article

Mathematical Olympiads for Undergrad Students

DSC Resources