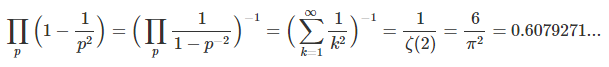We all know that, given two events A and B, the probability of the union A U B is given by the formula P(A U B) = P(A) + P(B) – P( AB) where AB represents the intersection of A and B. Most of us even know that
P(A U B U C) = P(A) + P(B) + P(C) – { P(AB) + P(AC) + P(BC) } + P(ABC)
In particular, if the events are independent, it becomes:
1 – P(A U B U C) = 1 – { P(A) + P(B) + P(C) } + { P(A)P(B) + P(A)P(C) + P(B)P(C) } – P(A)P(B)P(C)
This is equivalent to
1 – P(A U B U C) = { 1 – P(A) } { 1 – P(B) } { 1 – P(C) }
It generalizes to n independent events, and this formula is known as the inclusion-exclusion principle. Let us consider n events A(1), A(2), … , A(n) where A(k) is for a positive integer number, the property to be divisible by the square of the k-th prime number. We assume here that the first prime number is 2. These events are independent because we are dealing with prime numbers. As n tends to infinity, 1 – P( A(1) U A(2) U … U A(n) ) tends to the probability, for a positive integer number, to be square-free. Thus we have:
Beautiful Probability Theorem
The probability, for a positive integer number to be square-free (that is, not divisible by any square integer other than 1), is given by the formula below, where the product is over all prime numbers p > 1.
If you are interested in this kind of topic, read my article on number densities, especially the exercise at the bottom of section 1, and the section on probabilistic number theory at the bottom of section 4. You might also be interested in my article entitled the fundamental statistics theorem revisited.
Also, interestingly, the probability computed here is identical to the probability that two numbers are relatively prime.
Top DSC Resources
- Article: What is Data Science? 24 Fundamental Articles Answering This Question
- Article: Hitchhiker’s Guide to Data Science, Machine Learning, R, Python
- Tutorial: Data Science Cheat Sheet
- Tutorial: How to Become a Data Scientist – On Your Own
- Categories: Data Science – Machine Learning – AI – IoT – Deep Learning
- Tools: Hadoop – DataViZ – Python – R – SQL – Excel
- Techniques: Clustering – Regression – SVM – Neural Nets – Ensembles – Decision Trees
- Links: Cheat Sheets – Books – Events – Webinars – Tutorials – Training – News – Jobs
- Links: Announcements – Salary Surveys – Data Sets – Certification – RSS Feeds – About Us
- Newsletter: Sign-up – Past Editions – Members-Only Section – Content Search – For Bloggers
- DSC on: Ning – Twitter – LinkedIn – Facebook – GooglePlus
Follow us on Twitter: @DataScienceCtrl | @AnalyticBridge