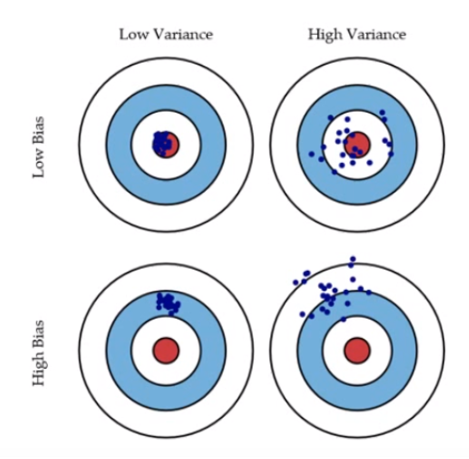
Intuition behind Bias-Variance trade-off, Lasso and Ridge Regression
Linear regression uses Ordinary Least square method to find the best coefficient estimates. One of the assumptions of Linear regression is that the variables are… Read More »Intuition behind Bias-Variance trade-off, Lasso and Ridge Regression