This is an unusual application of AI, it is not fiction, and it works! It started probably more than 30 years ago. Sometimes referred to as symbolic mathematics, and usually relying on high performance and high precision computing, it aims at automatically solving or computing, with an exact solution (not an approximation) complicated integrals, differential equations or systems of equations (including those involving complex numbers), identifying the exact value of some mathematical expressions, finding patterns in numbers, proving theorems that no mathematician has proved yet, and more. It is particularly useful in the context of experimental mathematics.
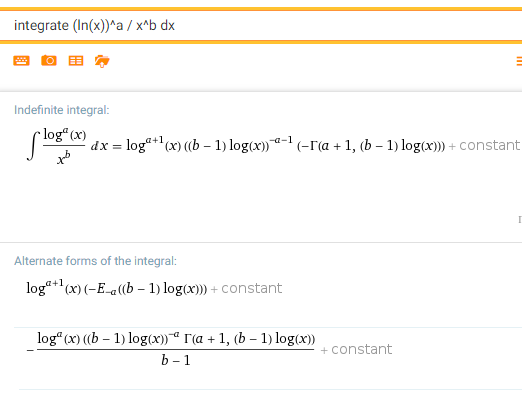
Example of symbolic math (see also this example)
It can do the work of students (high school and college) solving all their homework math problems in no time. Smart students already use it, as some of these tools are available online for free now, the most notorious one being WolframAlpha. I use it extensively when trying to find new results, see for example here, and it has cut my time, from discovery / making an assumption to proving a new result, by 80%.
Does it mean that mathematical research and education will become obsolete in the future, replaced by automated computations? No. In fact mathematical research will benefit from it: it will save professional mathematicians many hours of mundane work deriving and proving various tedious formulas, allowing them instead to focus exclusively on higher level mathematics, and not having to use graduate students to do the dirty work.
To this day, AI can’t solve all mathematical problems, and the solutions automatically computed sometimes make no sense. For instance, Wolfram Alpha is unable to compute the integrals featured in this article. And for some integrals, it returns a result that involves both the square root of an expression, and the square root of its opposite.
Another area where it is useful is to detect if a number, computed approximately up to 50 digits, corresponds to some known, exact mathematical constant. This is not a simple problem, the number could be a combination of multiple constants (for instance Pi^2 + e * log(5 + SQRT(5)). Also, sometimes two numbers agree up to 50 digits but are nevertheless different, and AI sometimes will figure this out. See the Wolfram entry on near integers, or the Wikipedia entry on mathematical coincidences.
Finally, if AI could write esoteric, jargon-filled papers to be submitted to scientific journals and read by 10 people at best, allowing university professors to write tons of papers effortlessly in order to get grants. It would help these mathematicians focus on real research and more interesting stuff. Automatically generated papers have already been accepted in prestigious math journals, see here. You can use this tool to generate such papers. However, for now, the success is not due to how smart the AI app writing these papers is, but rather, due to poor review performed by the reviewers.
Of course, there are basic questions that AI will never be able to answer in a long time, such as to whether or not the digits of SQRT(2) have a uniform distribution. My guess is that a human, not a robot, will be the first to answer that question with a solid proof.
To not miss this type of content in the future, subscribe to our newsletter. For related articles from the same author, click here or visit www.VincentGranville.com. Follow me on on LinkedIn, or visit my old web page here.
DSC Resources
- Book and Resources for DSC Members
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- Hire a Data Scientist | Search DSC | Find a Job
- Post a Blog | Forum Questions
