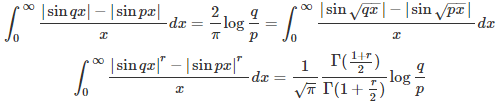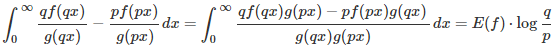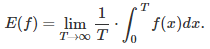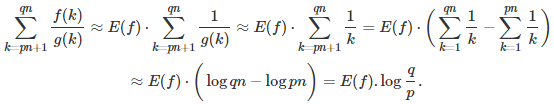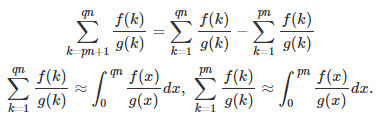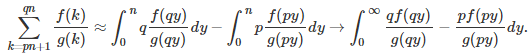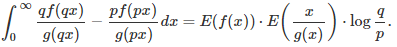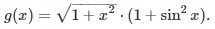Updated on Dec 12, 2018. An error was fixed when g(x) is not equal to x, and a new section “Generalization” was added. A link to a large collections of intriguing integrals was added at the bottom, in the “Related Problems” section.
Below are a few integrals that you won’t find in textbooks. Solving them is a good exercise for college students with some advanced calculus training. We provide the solution, as well as a general framework to compute many similar integrals. Maybe this material should be part of the standard math curriculum. Here, p, q, r are positive real numbers, with q larger than p.
The Gamma symbol represents the gamma function. It is possible that these results are published here for the first time. These are known as Frullani integrals, although the ones mentioned here are not covered by Frullani’s theorem, nor by any recent generalization that I am aware of (see here and here for recent contributions to this topic.) Indeed, AI-based automated integration platforms such as WolframAlpha can not find the exact value (only an approximation) while they are able to compute standard Frullani integrals exactly. My approach to derive the exact values is different from the classical approaches, as it relies on the statistical concept of expectation, possibly leading to interesting areas of research.
How to compute such integrals?
These integrals are a particular case of the following main result, proved in the next section:
where g(x) / x tends to 1 as x tends to infinity, and f is a bounded function with a finite expectation. Some additional conditions may be required, for instance the fact that the integral of f(x) / g(x), between 0 and 1, is finite. The expectation of f, also called average value, is defined as
For instance, if f(x) = |SIN(SQRT(x))|, then the expectation exists, and it is equal to E(f) = 2 / Pi. (Prove it!)
The main result introduced at the beginning of this section, is rather intuitive but needs great care to prove it rigorously, including correctly stating the required assumptions on f and g to make it valid. Some cases might require working with non-Riemann integrals. Here we only provide the intuitive explanation.
Proof of the main result (sketch)
Here p, q and n are integers, with q greater than p. We are interested in the case where n tends to infinity. We approximate integrals using the Euler-Maclaurin summation formula. The approximations below become equalities as n tends to infinity.
The first approximation is related to the Abelian theorem. We also used the classic approximation of the harmonic series to make the logarithm terms appear. Note that for large values of k, g(k) is asymptotically equal to k. This was one of the requirements for the formula to be valid.
Using the change of variable y = x / q in the first integral, and y = x / p in the second integral, we obtain:
This concludes the proof.
Note that for all the examples in the introduction, I used g(x) = x. I also tested it with different functions such as g(x) = x + 1, and it also worked. The results are not posted here.
Generalization
So far, we assumed that g(x) / x tends to 1 as x tends to infinity. What if instead, we make the more general assumption that g(x) / x, is equal to 1 on average? Using the notation E(f) or E(f(x)) interchangeably to denote the expectation of a function f, the main results becomes:
This formula works even if f or g is not Riemann-integrable, as long as the expectations are finite and different from zero. In this case, the integrals can be replaced by infinite sums or averages over equally-spaced points.
An example of function g not covered by the main theorem, but covered by its generalization, is
In this case, E(x / g(x)) = 1 / SQRT(2).
Discussion
While possibly the most important section in this article, I decided to put it at the bottom, hoping visitors will read this far. I did it on purpose, hoping some readers (I am thinking of college students or academics doing research on this topic) might find some apparent flaws in my “theorem”, and think deeper about the material presented here, especially about when my formula is right or wrong. I want them to discover it by themselves.
The most basic example is of course f(x) = 1 and g(x) = x. Why is my theorem not working in this case? Think about it before reading further. Answer: f(x) / g(x) is infinite in this case, if x = 0. Then you may ask, why is it working if f(x) = |SIN(SQRT(x))| and g(x) = x? Again think about it before reading further. Answer: while the convergence is very, very slow, in this case the integral of f(x) / g(x), say between 0 and 1, is finite. That is what makes this case different.
Another example where my theorem is not working is for the most classical Frullani integral, involving f(x) = exp(-x). In this historical case, the integral is driven by values around 0, rather than by large values of x (which is what my theorem was meant for.) Indeed, E(f) = 0 in this case. So in which cases is my theorem working? It certainly does if f is a periodic or almost-periodic function with bounded values, and with the integral of f(x) / g(x) between 0 and 1, being finite. So does it apply to f(x) = |SIN(SQRT(x))|? I believe so, but at this point, it is still a conjecture. Finding the largest class of functions that work is a very difficult problem. In the case of f(x) = |SIN(SQRT(x))|, WolframAlpha provides a good approximation until n is equal to 10,000 or so, then suddenly the approximated value sharply drops to zero. There is no doubt that WolframAlpha has it wrong, but that does not mean that I have it right.
Even in the case where it fails, the theorem can be amended. Instead of integrating between 0 and n, you you might want to integrate between 1 and n, to avoid the singularity. But this will change the formula — the only thing that needs to be updated is when I make the change of variables in the integration in the previous section. I invite you to make the amendment to discover what the updated (new) formula would be, in that case.
Final note
I was hoping to find some integrals with known exact value involving constants such as Pi, e, or SQRT(2) that would match the value computed using my formula involving log(q / p), to find simple relationships between these constants. This would have proved that some of these constants are redundant. But I was unable to find such relationships. This is still a great unsolved mathematical problem today. Are these constants related by a formula other than exp(i Pi) = -1? Nobody knows.
Related Problems
- Four Interesting Math Problems
- Curious Mathematical Problem
- Two Beautiful Mathematical Results – Part 2
- Two Beautiful Mathematical Results
- Number Theory: Nice Generalization of the Waring Conjecture
- Yet Another Interesting Math Problem – The Collatz Conjecture
- More Intriguing Integrals
To not miss this type of content in the future, subscribe to our newsletter. For related articles from the same author, click here or visit www.VincentGranville.com. Follow me on on LinkedIn, or visit my old web page here.
DSC Resources
- Book and Resources for DSC Members
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- Hire a Data Scientist | Search DSC | Find a Job
- Post a Blog | Forum Questions