Model evaluation metrics are used to assess goodness of fit between model and data, to compare different models, in the context of model selection, and to predict how predictions (associated with a specific model and data set) are expected to be accurate.
Confidence Interval. Confidence intervals are used to assess how reliable a statistical estimate is. Wide confidence intervals mean that your model is poor (and it is worth investigating other models), or that your data is very noisy if confidence intervals don’t improve by changing the model (that is, testing a different theoretical statistical distribution for your observations.) Modern confidence intervals are model-free, data -driven: click here to see how to compute them. A more general framework to assess and reduce sources of variance is called analysis of variance. Modern definitions of variance have a number of desirable properties.
Confusion Matrix. Used in the context of clustering. These N x N matrices (where N is the number of clusters) are designed as followed: the element in cell (i, j) represents the number of observations, in the test training set (as opposed to the control training set, in a cross-validation setting) that belong to cluster i and are assigned (by the clustering algorithm) to cluster j. When these numbers are transformed into proportions, these matrices are sometimes called contingency tables. A wrongly assigned observation is called false positive (non-fraudulent transaction erroneously labelled as fraudulent) or false negative (fraudulent transaction erroneously labelled as non- fraudulent). The higher the concentration of observations in the diagonal of the confusion matrix, the higher the accuracy / predictive power of your clustering algorithm.
Gain and Lift Chart. Lift is a measure of the effectiveness of a predictive model calculated as the ratio between the results obtained with and without the predictive model. Cumulative gains and lift charts are visual aids for measuring model performance. Both charts consist of a lift curve and a baseline. Click here for details.
Kolmogorov-Smirnov Chart. This non-parametric statistical test is used to compare two distributions, to assess how close they are to each other. In this context, one of the distributions is the theoretical distribution that the observations are supposed to follow (usually a continuous distribution with one or two parameters, such as Gaussian law), while the other distribution is the actual, empirical, parameter-free, discrete distribution computed on the observations.
Chi Square. It is another statistical test similar to Kolmogorov-Smirnov, but in this case it is a parametric test. It requires you to aggreate observations in a number of buckets or bins, each with at least 10 observations.
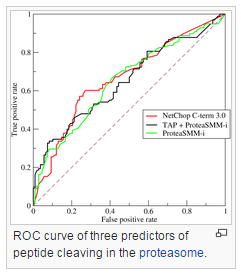
ROC curve. Unlike the lift chart, the ROC curve is almost independent of the response rate. The receiver operating characteristic (ROC), or ROC curve, is a graphical plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. The curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. The true-positive rate is also known as sensitivity or the sensitivity index d’, known as “d-prime” in signal detection and biomedical informatics, or recall in machine learning. The false-positive rate is also known as the fall-out and can be calculated as (1 – specificity). The ROC curve is thus the sensitivity as a function of fall-out. Click here for details.
Gini Coefficient. The Gini coefficient is sometimes used in classification problems. Gini = 2*AUC – 1, where AUC is the area under the curve (see the ROC curve entry above). A Gini ratio above 60% corresponds to a good model. Not to be confused with the Gini index or Gini impurity, used when building decision trees.
Root Mean Square Error. RMSE is the must used and abused metric to compute goodness of fit. It is defined as the square root of the absolute value of the correlation coefficient between true values and predicted values, and widely used by Excel users.
L^1 version of RSME. The RSME metric (see above entry) is an L^2 metric, sensitive to outliers. Modern metrics are L^1 and sometimes based on rank statistics rather than raw data. One of these new metrics, developed by our data scientist, is described here.
Cross Validation. This is a general framework to assess how a model will perform in the future; it is also used for model selection. It consists of splitting your training set into test and control data sets, training your algorithm (classifier, or predictive algorithm) on the control data set, and testing it on the test data set. Since the true values are known on the test data set, you can compare them with your predicted values, using one of the other comparison tools mentioned in this article. Usually the test data set itself is split into multiple subsets or data bins, to compute confidence intervals for predicted values. The test data set must be carefully selected, and must include different time frames and different types of observations (compared with the control data set), each with enough data points, in order to get sound, reliable conclusions as how the model will perform on future data, or on data that has slightly involved. Another idea is to introduce noise in the test data set and see how it impacts prediction: this is referred to as model sensitivity analysis.
Predictive Power. This metric was developed internally at Data Science Central by our data scientist. It is related to the concept of entropy or the Gini index mentioned above in this article. It was designed as a synthetic metric satisfying interesting properties, and used to select a good subset of features in any machine learning project, or as a criterion to decide which node to split at each iteration, when building decision trees. Click here for details.
DSC Resources
- Career: Training | Books | Cheat Sheet | Apprenticeship | Certification | Salary Surveys | Jobs
- Knowledge: Research | Competitions | Webinars | Our Book | Members Only | Search DSC
- Buzz: Business News | Announcements | Events | RSS Feeds
- Misc: Top Links | Code Snippets | External Resources | Best Blogs | Subscribe | For Bloggers
Additional Reading
- What statisticians think about data scientists
- Data Science Compared to 16 Analytic Disciplines
- 10 types of data scientists
- 91 job interview questions for data scientists
- 50 Questions to Test True Data Science Knowledge
- 24 Uses of Statistical Modeling
- 21 data science systems used by Amazon to operate its business
- Top 20 Big Data Experts to Follow (Includes Scoring Algorithm)
- 5 Data Science Leaders Share their Predictions for 2016 and Beyond
- 50 Articles about Hadoop and Related Topics
- 10 Modern Statistical Concepts Discovered by Data Scientists
- Top data science keywords on DSC
- 4 easy steps to becoming a data scientist
- 22 tips for better data science
- How to detect spurious correlations, and how to find the real ones
- 17 short tutorials all data scientists should read (and practice)
- High versus low-level data science
Follow us on Twitter: @DataScienceCtrl | @AnalyticBridge