Product of two large primes are at the core of many encryption algorithms, as factoring the product is very hard for numbers with a few hundred digits. The two prime factors are associated with the encryption keys (public and private keys). Here we describe a new approach to factoring a big number that is the product of two primes of roughly the same size. It is designed especially to handle this problem and identify flaws in encryption algorithms.
While at first glance it appears to substantially reduce the computational complexity of traditional factoring, at this stage there is still a lot of progress needed to make the new algorithm efficient. An interesting feature is that the success depends on the probability of two numbers to be co-prime, given the fact that they don’t share the first few primes (say 2, 3, 5, 7, 11, 13) as common divisors. This probability can be computed explicitly and is about 99%.
The methodology relies heavily on solving systems of congruences, the Chinese Remainder Theorem, and the modular multiplicative inverse of some carefully chosen integers. We also discuss computational complexity issues. Finally, the off-the-beaten-path material presented here leads to many original exercises or exam questions for students learning probability, computer science, or number theory: proving the various simple statements made in my article.
1. Some Number Theory Explained in Simple English
You may skip this section. Here I outline the theory used to derive the main results in the next sections. The level is barely above high school (except for section 1.2), yet usually not taught even in many college math curricula.
1.1. Co-primes and pairwise co-primes. The first concept is that of co-prime numbers. Two numbers are co-prime if they don’t share a common divisor, for instance, 15 and 14. Three numbers are pairwise co-prime if no two of them share a common divisor, for instance, 3, 4 and 7. To the contrary, 3, 4 and 6 are co-prime (no common divisor) but not pair-wise co-prime, as 3 and 6 share a common divisor.
1.2. Probability of being co-prime. If p and q are primes, then the probability for a number to be divisible by p is independent of that of being divisible by q. For two numbers to be co-prime, they most not share any prime divisors, thus the probability is equal to
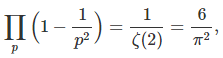
where the product is over all primes, and ζ is the Rienman zeta function. See here for a more rigorous proof. Likewise, the probability that k random numbers are co-prime (though not necessarily pair-wise co-prime) is 1/ ζ(k). See here for details. The probability that k random numbers are pair-wise co-prime is
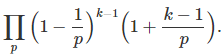
Again, the product is over all primes. When k = 2, the two formula are identical. A proof can be found here.
1.3. Modular multiplicative inverse. The notation a = b Mod c, for positive integers with b < c, means that | a – b | divides c. The modular multiplicative inverse of a (modulo c) is the positive integer d satisfying ad = 1 Mod c and d < c. It exists and is unique if and only if a and d are co-prime.
1.4. Chinese remainder theorem, version A.
This fundamental result is a consequence of the Chinese remainder theorem.
If z is not a prime number, then the following system of k congruences, with xy ≤ z, uniquely determines two non-trivial numbers x, y such that xy = z. In other words, it allows you to find two factors x, y of z. The system is as follows:
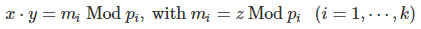
Here p1, …, pk must be pair-wise co-prime and their product larger than z.
1.5. Chinese remainder theorem, version B.
This is a particular case of the Chinese remainder theorem, also useful in our context.
Let p1, …, pk be k pairwise co-prime positive integers, and a > 0 an integer. If z = a Mod pi for i = 1,⋯, k, then z = a Mod (p1 p2 ⋯ pk).
More about this can be found here.
2. The New Factoring Algorithm
The basic idea is to replace the difficult problem of solving xy = z (assuming here that x and y are two large prime numbers) by a system of congruences accepting more solutions, thus easier to solve. However, so far, no efficient way of solving these congruences has been found.
2.1. Improving computational complexity
Indeed xy = z can be seen as a congruence, namely xy = m Mod z, with m = 0. Thus the problem of factoring z is treated as a particular case of solving a congruence, with the residue m equal to 0, and the moduli equal to z. Let us assume that the computational complexity to solve this congruence is O(f(z)) for some function f. The computational complexity is a function of z (as z gets large) but is thought to be independent of m. Using the most inefficient algorithm, we would have f(z) = SQRT(z). If we manage to split this congruence in (say) two smaller ones each with a moduli close to SQRT(z), then we are reducing the computational complexity from O(f(z)) to O(f(SQRT(z))). And this can be carried out recursively until we end up with congruences that all have small moduli. This is the basic principle governing our approach.
More about computational complexity is discussed in exercise 2, at the bottom of section 3.
2.2. Five-step algorithm
As an illustration of how the algorithm works, let’s apply it to factoring a very modest number, z = xy = 1223 × 2731. It involves the following steps.
Step 1. Compute f(p) = z Mod p, for p = 2, 3, 5, 7, 9, 11, 13,…, M. The upper bound M is discussed later; it is a very small number compared to z. Check values of p generating many identical values of f(p). Here, f(p) = 5 or f(p) = 23 for instance.
Step 2. We have f(59) = f(85) = f(111) = 23. By virtue of theorem B (see section 1.5), we also have f(59 × 85 × 111) = 23. I am not sure yet if this is of any help.
Step 3. Find the set of couples (x, y) with x < y, with x, y odd, and xy ≤ z satisfying all of the following:
- xy =23 Mod 59
- xy =23 Mod 85
- xy =23 Mod 111
You need to create 3 multiplication tables to identify the full list (intersection of 3 infinite lists) of candidates, and ignore those (x, y) that result in xy > z or x even or y even.
Step 4. The result is (x, y) ∈ { (61, 36503), (173, 12871), (211, 10553), (829, 1327), (1223, 2731) }. The code below shows how these couples were produced. The % symbol in the code represents the modulo operator.

Step 5. Among all the 5 above candidates, check if one yields xy = z. Here (x = 1223, y = 2731) does and we’ve factored z.
How to determine M? You want M as small as possible, but large enough so that you have enough low p‘s with identical f(p) — in our case, p = 59, p = 85 and p = 111 — and such that their product is of the same order of magnitude as z.
If instead, we consider 5 congruences rather than 3, say
- xy = 5 Mod 21
- xy = 5 Mod 47
- xy = 23 Mod 59
- xy = 23 Mod 85
- xy = 23 Mod 111
then there would be only one candidate in step 4, resulting in factoring z. Note that the product 21 × 47 × 59 × 85 × 111 = 549,428,355 is big enough (much bigger than z itself) and this is what causes the candidate in step 4 to be unique, thus removing the need for step 5.
Another example also producing a single candidate (the correct one) is
- xy = 2 Mod 3
- xy = 3 Mod 5
- xy = 5 Mod 7
- xy = 6 Mod 11
- xy = 1 Mod 13
- xy = 6 Mod 17
- xy = 3 Mod 19
Again only one candidate in step 4 (thus no step 5) because 3 × 5 × 7 × … × 19 = 4,849,845 is big enough, bigger than z.
2.3. Probabilistic optimization
Here I discuss a different approach to selecting the congruences. Let us continue to work with the same example: z = xy = 1223 × 2731. Take two co-prime moduli p1, p2 very close to SQRT(z) and it also works. For instance, with p1 = 1827, p2 = 1829, we have:
- xy = 257 Mod 1827
- xy = 259 Mod 1829
There is only one solution to this, it’s x = 1223, y = 2731, revealing two factors of z. It works here because by chance, 1827 and 1829 are co-prime. To increase the chances that the two moduli are co-prime, one can choose p1 = 2 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ q1 + 1 and p2 = 11 ⋅ 13 ⋅ q2 + 2, where q1, q2 are as small as possible yet satisfying p1 ⋅ p2 > z. Here q1 = 9 and q2 = 13 works, resulting in p1 = 1891 and p2 =1861. Again this leads to a unique (correct) solution in step 4. And by construction, we know that p1, p2 do not share any of 2, 3, 5, 7, 11, 13 as common divisors, making it much more likely that they are co-prime (indeed, they are). In this case, x, y satisfy
- xy = 507 Mod 1891
- xy = 1379 Mod 1861
The only solution with x ⋅ y ≤ z and x < y is again x = 1223, y = 2731. Again, x ⋅ y = z. The probability that two numbers not sharing 2, 3, 5, 7, 11, 13 as common divisors are co-prime, is
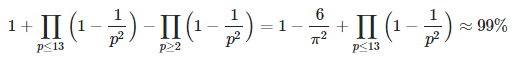
See section 1.2 for more details; the products are over primes only. By contrast, the probability that two random numbers are co-prime without the above restriction, is about 61%. When working with co-prime moduli, theorem A applies thus guaranteeing a unique solution (see section 1.4.) The last two congruences (xy = 507 Mod 1891 combined with xy = 1379 Mod 1861) are supposed to significantly reduce the computational complexity of the initial problem of factoring z, that is, finding x, y such that xy = 0 Mod 3340013. Both problems are equivalent. Note that z = 3340013.
Instead of using two co-prime close to SQRT(z), you could use four pair-wise co-prime close to z^(1/4), for instance:
- xy = 30 Mod 41
- xy = 31 Mod 43
- xy = 23 Mod 45
- xy = 5 Mod 47
This works too by virtue of theorem A in section 1.4. Is it more efficient?
3. Compact Formulation of the Problem
Let’s focus on the case z = xy with
- xy = m1 Mod p1
- xy = m2 Mod p2
Here p1, p2 are co-prime, and p1 ⋅ p2 > z. We further assume that z is a product of two large primes, and that p1 ≈ p2 ≈ SQRT(z), so that x < min(p1, p2).
The above example with z = 3340013, p1 = 1891, p2 = 1861 is a typical case satisfying these requirements. It results, as discussed earlier, in m1 = 507, m2 = 1379. The solution is x = 1223, y = 2731. The methodology below uses that example as an illustration.
Let us denote as Gp(y) the modular multiplicative inverse of y, modulo p, as described in section 1.3.That is, Gp(y) is uniquely defined by 0 < Gp(y) < p and y ⋅ Gp(y) = 1 Mod p. This inverse exists if and only if y and p are co-prime. It can be computed using the extended Euclidean algorithm. Then the above system with two variables x, y and two congruences xy = m1 Mod p1, xy = m2 Mod p2 simplifies to one equation with one variable (unknown) y, as follows:
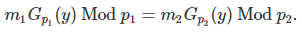
This is a strict equality, not a “modulo equality”. The big challenge is how to solve this equation efficiently. Here we show that this equation is correct for our example. If p1 = 1891, p2 = 1861, y = 2731, then we have Gp1(y) = 1416 and Gp2(y) = 1538. We also have
507⋅1416 Mod 1891 = 1223 = 1379 ⋅1538 Mod 1861.
So the equation is satisfied. Note that 1223 = x, the other factor of z. This is always the case. Also if you know Gp1(y), you can easily retrieve y by performing another modular inversion: y = Gp1(Gp1(y)) + n⋅p1 where n > 0 is a small integer assuming x, y are relatively close to each other. In our case, Gp1(Gp1(y)) = Gp1(1416) = 840 and n = 1, yielding y = 840 + 1891 = 2731. Likewise, if you know Gp2(y), you can also retrieve y.
Exercises
[1] Find all x, y such that xy = 3 Mod 7. Solution:
- x = 1 Mod 7 and y = 3 Mod 7, or
- x = 2 Mod 7 and y = 5 Mod 7, or
- x = 3 Mod 7 and y = 1 Mod 7, or
- x = 4 Mod 7 and y = 6 Mod 7, or
- x = 5 Mod 7 and y = 2 Mod 7, or
- x = 6 Mod 7 and y = 4 Mod 7.
[2] Solving an equation such as xy = m Mod p requires the computation of the modular multiplication table modulo p, that is (p – 1)^2 operations, see exercise [1]. If you need to solve k such equations with k pair-wise coprime moduli p1, …, pk, then the number of operations is
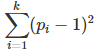
Compare the number of operations for the 3 following cases investigated in this article:
- p1 = 1891, p2 = 1861
- p1 = 41, p2 = 43, p3 = 45, p4 = 47
- p1 = 3, p2 = 5, p3 = 7, p4 = 11, p5 = 13, p6 = 17, p7 = 19
Now a difficult question. If we choose, for the moduli, the k smallest primes p1, p2, …, pk such that their product is barely larger than z, how many operations are needed asymptotically as z becomes larger and larger? Solution: the number of operations grows more slowly than A (log z)^B where A, B are two constants, with B as low as 3 or maybe even as low as 2.75.
To put this into perspective, to factor all the positive integers up to 10^300, you only need to perform 2 x 10^7 operations to produce all the necessary modular multiplication tables. Then for each table (say for p) you only need to store p – 1 data points (see exercise 1, where p = 7), thus the total storage required is about 42,000 integers, with the largest of these integers being smaller than 800. And because of the symmetry of the multiplication, you can do with half that storage, that is 21,000 integers. In fact, you only need to consider the first k = 130 prime numbers, the largest of them being less than 800.
4. Other Math Articles by Same Author
Here is a selection of articles pertaining to experimental math and probabilistic number theory:
- Statistics: New Foundations, Toolbox, and Machine Learning Recipes
- Applied Stochastic Processes
- Variance, Attractors and Behavior of Chaotic Statistical Systems
- New Family of Generalized Gaussian Distributions
- A Beautiful Result in Probability Theory
- Two New Deep Conjectures in Probabilistic Number Theory
- Extreme Events Modeling Using Continued Fractions
- A Strange Family of Statistical Distributions
- Some Fun with Gentle Chaos, the Golden Ratio, and Stochastic Number…
- Fascinating New Results in the Theory of Randomness
- Two Beautiful Mathematical Results – Part 2
- Two Beautiful Mathematical Results
- Number Theory: Nice Generalization of the Waring Conjecture
- Fascinating Chaotic Sequences with Cool Applications
- Simple Proof of the Prime Number Theorem
- Factoring Massive Numbers: Machine Learning Approach
