This is another spectacular property of the exponential distribution, and also the first time an explicit formula is obtained for the variance of the range, besides the uniform distribution. It has important consequences, and the result is also useful in applications.
Theorem
The range R(n) associated with n independent random variables with an exponential distribution of parameter l satisfies
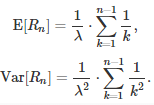
Before proving the theorem, note that the first formula is well known, only the second one is new. The standard proof for the expectation is not considered simple: it is based on computing the expectation for the maximum (see here) and the fact that the minimum also has an exponential distribution with known expectation (see here). Our proof is simpler and also covers the variance.
Proof
The general distribution of the range is known for any distribution, see here. The range is defined as
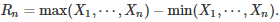
In the case of the exponential distribution, the range computed on n random variables has the following density (see here page 3):
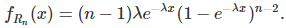
With a simple change of variable, the k-th moment of the range is equal to
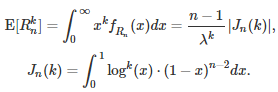
Using WolframAlpha (see here and here) one obtains
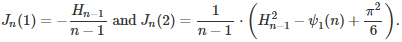
Thus,
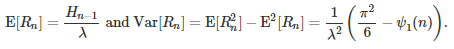
The two symbols H(n-1) and ψ1(n) represent the harmonic numbers and the Trigamma function, respectively. To complete the proof, use the fact that
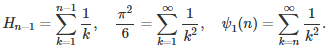
∎
There are a number of interesting consequences to this result. First, the expectation of the range grows indefinitely and is asymptotically equal to log(n). Also, the variance of the range grows slowly and eventually converges to p^2 / 6. This is in contrast to the uniform distribution: its range is bounded, and its variance tends to zero as fast as 1 / n^2, see section 2.3 in this article.
This result is pretty deep. It is almost like the range, for the exponential distribution, is made up of a weighted sum of independent exponential variables with same parameter λ, with the k-th term added into the sum contributing with a weight equal to 1 / k.
But perhaps most importantly, we found the two extreme cases to a new statistical theorem (see here, section 1) stating that the length of any confidence interval attached to an estimator is asymptotically equal to A / n^B, with B between 0 and 1. This length is usually proportional to the standard deviation of the estimator in question. In practice, in almost all cases, B = 1/2. However, here we have:
- For the range, if the variables are independently and uniformly distributed, then B = 1.
- For the range, if the variables are independent with exponential distribution, then B = 0.
For normal variables, Var[Range] = O(1/n) and E[Range] = O(SQRT(log n)), thus B = 1/2 (see here and here.) These results are summarized in the table below:
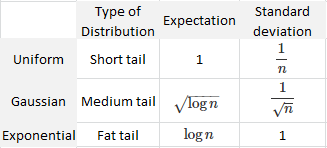
Order of magnitude for the expectation and Stdev of the range
Finally, the same technique could be used to compute higher moments, or to compute the variance of the range for other probability distributions. It could also help with studying the convergence of the re-scaled range and its associated Hurst exponent, see section 6.1 in this article for details.
To not miss this type of content in the future, subscribe to our newsletter. For related articles from the same author, click here or visit www.VincentGranville.com. Follow me on on LinkedIn, or visit my old web page here.
