In this article, we revisit the most fundamental statistics theorem, talking in layman terms. We investigate a special but interesting and useful case, which is not discussed in textbooks, data camps, or data science classes. This article is part of a series about off-the-beaten-path data science and mathematics, offering a fresh, original and simple perspective on a number of topics. Previous articles in this series can be found here and also here.
The theorem discussed here is the central limit theorem. It states that if you average a large number of well behaved observations or errors, eventually, once normalized appropriately, it has a standard normal distribution. Despite the fact that we are dealing here with a more advanced and exciting version of this theorem (discussing the Liapounov condition), this article is very applied, and can be understood by high school students.
In short, we are dealing here with a not-so-well-behaved framework, and we show that even in that case, the limiting distribution of the “average” can be normal (Gaussian.). More precisely, we show when it is and when it is not normal, based on simulations and non-standard (but easy to understand) statistical tests.
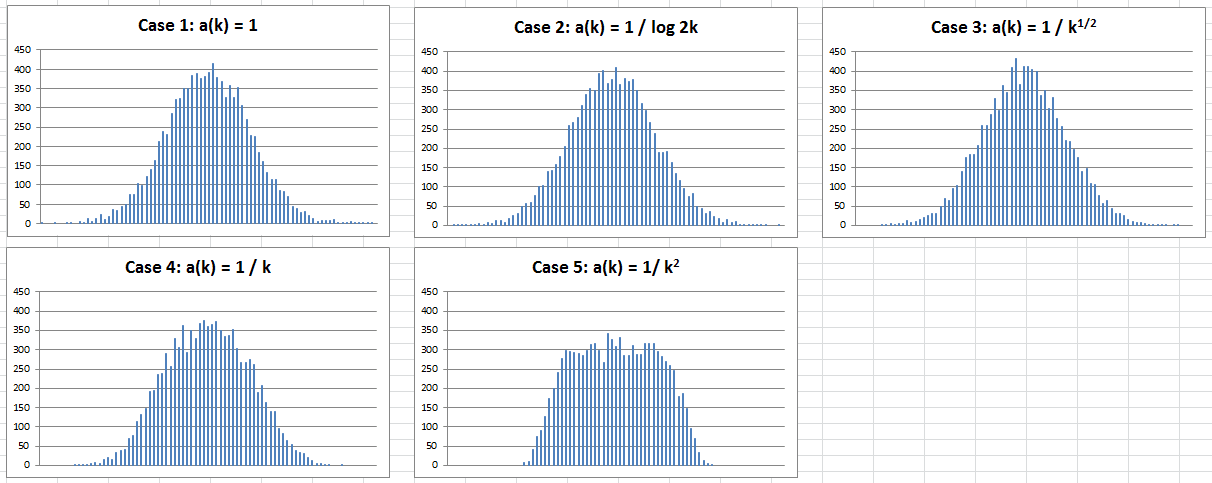
Figure 1: The first three cases show convergence to the Gaussian distribution
(click on picture to zoom in)
1. A special case of the Central Limit Theorem
Let’s say that we have n independent observations X(1),…, X(n) and we compute a weighted sum
S = a(1) X(1) + … + a(n) X(n).
Under appropriate conditions to be discussed later, (S – E(S) ) / Stdev(S) has a normal distribution of mean 0 and variance 1. Here E denotes the expectation and Stdev denotes the standard deviation, that is, the square root of the variance.
This is a non-basic case of the central limit theorem, as we are dealing with a weighted sum. The classic, basic version of the theorem assumes that all the weights a(1),…,a(n) are equal. Furthermore, we focus here on the particular case where
- The highest weights (in absolute value) are concentrated on the first few observations,
- The weight a(k) tends to 0 as k tends to infinity.
The surprising result is the fact that even with putting so much weight on the first few observations, depending on how slowly a(k) converges to 0, the limiting distribution is still Gaussian.
About the context
You might wonder: how is this of any practical value in the data sets that I have to process in my job? Interestingly, I started to study this type of problems long ago, in the context of k-NN (nearest neighbors) classification algorithms. One of the questions, to estimate the local or global intensity of a stochastic point process, and also related to density estimation techniques, was: how many neighbors should we use, and which weights should we put on these neighbors to get robust and accurate estimates? It turned out that putting more weight on close neighbors, and increasingly lower weight on far away neighbors (with weights slowly decaying to zero based on the distance to the neighbor in question) was the solution to the problem. I actually found optimum decaying schedules for the a(k)’s, as k tends to infinity. You can read the detail here.
2. Generating data, testing, and conclusions
Let’s get back to the problem of assessing when the weighted sum S = a(1) X(1) + … + a(n) X(n), after normalization, converges to a Gaussian distribution. By normalization, I mean considering (S – E(S) ) / Stdev(S) instead of S.
In order to solve this problem, we performed simulations as follows:
Simulations
Repeat m = 10,000 times:
- Produce n = 10,000 random deviates X(1),…,X(n) uniformly distrubuted on [0, 1]
- Compute S = a(1) X(1) + … + a(n) X(n) based on a specific set of weights a(1),…,a(n)
- Compute the normalized S, denoted as W = (S – E(S) ) / Stdev(S).
Each of the above m iterations provides one value of the limiting distribution. In order to investigate the limiting distribution (associated with a specific set of weights), we just need to look at all these m values, and see whether they behave like deviates from a Gaussian distribution of mean 0 and variance 1. Note that we found n = 10,000 and m = 10,000 to be large enough to provide relatively accurate results. We tested various values of n before settling for n = 10,000, looking at what (little) incremental precision we got from increasing n (say) from 500 to 2,000 and so on. Also note that the random number generator is not perfect, and due to numerical approximations made by the computer, indefinitely increasing n (beyond a certain point) is not the solution to get more accurate results. That said, since we investigated 5 sets of weights, we performed 5 x n x m = 500 million computations in very little time. A value of m = 10,000 provides about two correct digits when computing the percentiles of the limiting distribution (except for the most extreme ones), provided n is large enough.
The source code is provided in the last section.
Analysis and results
We tested 5 sets of weights, see Figure1:
- Case 1: a(k) = 1, corresponding to the classic version of the Central Limit Theorem, and with guaranteed convergence to the Gaussian distribution.
- Case 2: a(k) = 1 / log 2k, still with guaranteed convergence to the Gaussian distribution
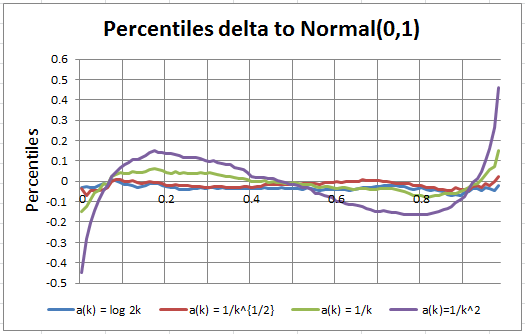
- Case 3: a(k) = k^{-1/2}, the last exponent (-1/2) that still provides guaranteed convergence to the Gaussian distribution, according to the Central Limit Theorem with the Liapounov condition (more on this below.) A value below -1/2 violates the Liapounov condition.
- Case 4: a(k) = k^{-1}, the limiting distribution looks Gaussian (see Figure 1) but it is too thick to be Gaussian, indeed the maximum is also too low, and the kurtosis is now significantly different from zero, thus the limiting distribution is not Gaussian (though almost).
- Case 5: a(k) = k^{-2}, not converging to the Gaussian distribution, but instead to an hybrid continuous distribution, half-way Gaussian, half-way uniform.
Note that by design, all normalized S’s have mean 0 and variance 1.
We computed (in Excel) the percentiles of the limiting distributions for each of the five cases. Computations are found in this spreadsheet. We compared the cases 2 to 5 with case 1, computing the differences (also called deltas) for each of the 100 percentiles. Since case 1 corresponds to a normal distribution, we actually computed the deltas to the normal distribution, see Figure 2. The deltas are especially large for the very top or very bottom percentiles in cases 4 and 5. Cases 2 and 3 show deltas close to zero (not statistically significantly different from zero), and this is expected since these cases also yield a normal distribution. To assess the statistical significance of these deltas, one can use the model-free confidence interval technique described here: it does not require any statistical or probability knowledge to understand how it works. Indeed you don’t even need a table of the Gaussian distribution for testing purposes here (you don’t even need to know what a Gaussian distribution is) as case 1 automatically provides one.
The Liapounov connection
For those interested in the theory, the fact that cases 1, 2 and 3 yield convergence to the Gaussian distribution is a consequence of the Central Limit Theorem under the Liapounov condition. More specifically, and because the samples produced here come from uniformly bounded distributions (we use a random number generator to simulate uniform deviates), all that is needed for convergence to the Gaussian distribution is that the sum of the squares of the weights — and thus Stdev(S) as n tends to infinity — must be infinite. This result is mentioned in A. Renyi’s book Probability Theory (Dover edition, 1998, page 443.)
Note that in cases 1, 2, and 3 the sum of the squares of the weights is infinite. In cases 4 and 5, it is finite, respectively equal to Pi^2 / 6 and Pi^4 / 90 (see here for details.) I am very curious to know what the limiting distribution is for case 4. Can anyone provide some insights?
3. Generalizations
Here we discuss generalizations of the central limit theorem, as well as potential areas of research
Generalization to correlated observations
One of the simplest ways to introduce correlation is to define a stochastic auto-regressive process using
Y(k) = p Y(k-1) + q X(k)
where X(1), X(2), … are independent with identical distribution, with Y(1) = X(1) and where p, q are positive integers with p + q =1. The Y(k)’s are auto-correlated, but clearly, Y(k) is a weighted sum of the X(j)’s (1<= j <= k), and thus, S = a(1) Y(1) + … + a(n) Y(n) is also a weighted sum of the X(k)’s, with higher weights on the first X(k)’s. Thus we are back to the problem discussed in this article, but convergence to the Gaussian distribution will occur in fewer cases due to the shift in the weights.
More generally, we can work with more complex auto-regressive processes with a covariance matrix as general as possible, then compute S as a weighted sum of the X(k)’s, and find a relationship between the weights and the covariance matrix, to eventually identify conditions on the covariance matrix that guarantee convergence to the Gaussian destribution.
Generalization to non-random (static) observations
Is randomness really necessary for the central limit theorem to be applicable and provable? What about the following experiment:
- Compute all unordered sums S made up of n integers, 0 or 1, with repetitons allowed. For instance, if n = 2, the four possibilities are 0+0, 0+1, 1+0, 1+1. For an arbitrary n, we have 2^n possibilities.
- Normalize S as usual. For normalization, here use E(S) = n / 2 and Stdev(S) = SQRT(n) / 2.
Do these 2^n normalized values of S (generated via this non-random experiment) follow a Gaussian distribution as n tends to infinity? Ironically, one way to prove that this is the case (I haven’t checked if it is the case or not, but I suspect that it is) would be to randomly sample m out of these 2^n values, and then apply the central limit theorem to the randomly selected values as m tends to infinity. Then by increasing m until m is as large as 2^n we would conclude that the central limit theorem also holds for the non-random (static) version of this problem. The limiting distribution definitely has a symmetric, bell-like shape, just like the Gaussian distribution, though this was also the case in our above “case 4” example — yet the limit was not Gaussian.
Other interesting stuff related to the Central Limit Theorem
There is a lot of interesting stuff on the Wikipedia entry, including about the Liapounov condition. But the most interesting things, at least in my opinion, were the following:
- The area S of a convex hull of n points X(1),…,X(n) also converges to a normal distribution, once standardized, that is when considering (S – E(S)) / Stdev(S).
- Under some conditions, the result below applies, with C being a universal constant:
- If instead of a weighted average S, we consider the maximum M = max(X(1),…,X(n)), then we also have a limiting distribution for (M – E(M)) / Stdev(M) after proper standardization. This is known as the Fisher–Tippett–Gnedenko theorem in extreme value theory. The limit distribution is not Gaussian. What would happen if instead of the maximum or weighted average, we consider the empirical percentiles?
- The digits for the vast majority of numbers, in all number representation systems, can be used to emulate Brownian motions, thanks to the central limit theorem. For details, read this article.
Another potential generalization consists of developing a central limit theorem that is based on L^1 rather than L^2 measures of centrality and dispersion, that is, the median and absolute deviations rather than the mean and variance. This would be useful when the observations come from a distribution that does not have a mean or variance, such as Cauchy.
Also, does the limit distribution in case 4 depend on the distribution of the X(k)’s — in this case uniform — or is it a universal distribution that is the same regardless of the X(k)’s distribution? Unfortunately, the answer is negative: after trying with the square of uniform deviates for the X(k)’s, the limit distribution was not symmetric, and thus different from the one obtained with uniform deviates.
4. Appendix: source code and chart
Below is the source code (Perl) used to produce the simulations:
$seed=100;
$c=-0.5; # the exponent in a(k) = k^c
$n=10000;
open(OUT,”>out.txt”);
for ($m=0; $m<10000; $m++) {
$den=0;
$num=0;
$ss=0;
for ($k=1; $k<=$n; $k++) {
$r=rand();
$aux=exp($c*log($k)); # k^c
$num+=$r*$aux;
$den+=$aux;
$ss+=($aux*$aux);
}
$dev=$num/$den;
$std=sqrt(1/12) * (sqrt($ss)/$den); # 1/12 for Uni[0,1]
$dev2=($dev-0.5)/$std;
print OUT “$m\t$dev2\n”;
}
close(OUT);
Also, Figure 2 below is referenced earlier in this article.
Figure 2: Two of the weight sets clearly produce non-Gaussian limit distributions
Top DSC Resources
- Article: What is Data Science? 24 Fundamental Articles Answering This Question
- Article: Hitchhiker’s Guide to Data Science, Machine Learning, R, Python
- Tutorial: Data Science Cheat Sheet
- Tutorial: How to Become a Data Scientist – On Your Own
- Categories: Data Science – Machine Learning – AI – IoT – Deep Learning
- Tools: Hadoop – DataViZ – Python – R – SQL – Excel
- Techniques: Clustering – Regression – SVM – Neural Nets – Ensembles – Decision Trees
- Links: Cheat Sheets – Books – Events – Webinars – Tutorials – Training – News – Jobs
- Links: Announcements – Salary Surveys – Data Sets – Certification – RSS Feeds – About Us
- Newsletter: Sign-up – Past Editions – Members-Only Section – Content Search – For Bloggers
- DSC on: Ning – Twitter – LinkedIn – Facebook – GooglePlus
Follow us on Twitter: @DataScienceCtrl | @AnalyticBridge