For a person being from a non-statistical background the most confusing aspect of statistics, are always the fundamental statistical tests, and when to use which. This blog post is an attempt to mark out the difference between the most common tests, the use of null value hypothesis in these tests and outlining the conditions under which a particular test should be used.
Null Hypothesis and Testing
Before we venture on the difference between different tests, we need to formulate a clear understanding of what a null hypothesis is. A null hypothesis, proposes that no significant difference exists in a set of given observations. For the purpose of these tests in general
- Null: Given two sample means are equal
- Alternate: Given two sample means are not equal
For rejecting or accepting a null hypothesis, a test statistic is calculated. This test-statistic is then compared with a critical value and if it is found to be greater than the critical value the hypothesis is rejected. “In the theoretical underpinnings, hypothesis tests are based on the notion of critical regions: the null hypothesis is rejected if the test statistic falls in the critical region. The critical values are the boundaries of the critical region. If the test is one-sided (like a χ2 test or a one-sided t-test) then there will be just one critical value, but in other cases (like a two-sided t-test) there will be two.”
This article also discusses critical value, and the following tests:
- Z-test
- T-test
- Anova and F-test
- Chi-Square test
Read full article here. 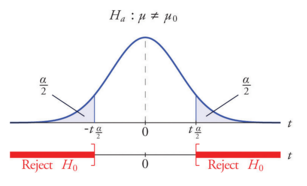
DSC Resources
- Invitation to Join Data Science Central
- Free Book: Applied Stochastic Processes
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Post a Blog | Forum Questions
