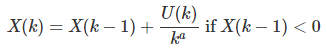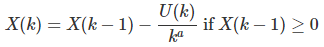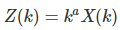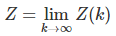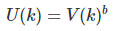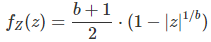Announcement: Winner of the Data Science Central Competition

Back in 2017, we posted a problem related to stochastic processes and controlled random walks, offering a $2,000 award for a sound solution, see here for full details. The problem, which had a FinTech flavor, was only solved recently (December 2018) by Victor Zurkowski.

About the problem:

Let’s start with X(1) = 0, and define X(k) recursively as follows, for k > 1:

and let’s define U(k), Z(k), and Z as follows:

where the V(k)’s are deviates from independent uniform variables on [0, 1].

So there are two positive parameters in this problem, a and b, and U(k) is always between 0 and 1. When b = 1, the U(k)’s are just standard uniform deviates, and if b = 0, then U(k) = 1. The case a = b = 0 is degenerate and should be ignored. The case a > 0 and b = 0 is of special interest, and it is a number theory problem in itself, related to this problem when a = 1. Also, just like in random walks or Markov chains, the X(k)’s are not independent; they are indeed highly auto-correlated.

Prove that if a < 1, then X(k) converges to 0 as k increases. Under the same condition, prove that the limiting distribution Z

always exists, (Note: if a > 1, X(k) may not converge to zero, causing a drift and asymmetry)
always takes values between -1 and +1, with min(Z) = -1 and max(Z) = +1,
is symmetric, with mean and median equal to 0
and does not depend on a, but only on b.

For instance, for b =1, even a = 0 yields the same triangular distribution for Z, as any a > 0.

Main question: In general, what is the limiting distribution of Z? I guessed, using empirical data science techniques such as model fitting, simulations, and goodness-of-fit tests, that the solution (which implied solving a stochastic integral solution) was, with z in [-1. 1]:

About the author and the solution:

Victor not only confirmed that the above density function is a solution to this problem, but also that the solution is unique, focusing on convergence issues, in a 27-page long paper. One detail still needs to be worked out: whether or not scaled Z visits the neighborhood of every point in [-1,1] infinitely often. Victor believes that the answer is positive. You can read his solution here, and we hope it will result in a publication in a scientific journal.

Victor Zurkowski, PhD, is a predictive modeling, machine learning, and optimization expert with 20+ years of experience, with deep expertise developing pricing models and optimization engines across industries, including Retail, Financial Services. He published various academic papers in Mathematics and Statistics across numerous topics, and is currently VP of Data Science at Polymatiks. Victor holds a Ph.D. in Mathematics from the University of Minnesota and an M.Sc. in Statistics from the University of Toronto.

DSC Resources