Using unsupervised learning to improve prediction performance

Even if they could deliver on a crystal ball, such a capability would obviously have enormous consequences for all aspects of human existence. In truth, even small steps in this direction have major implications for society at large, as well as for specific industries and other entities.   

Chief among the methods for prediction is regression (linear and logistic), often highly tuned to the specific environment. There are dozens of others, however, including deep learning, support vector machines and decision trees.

Many of these methods have as their output the estimate of a particular quantity, such as a stock price, the outcome of an athletic contest or an election, either in binary terms (who wins and who loses) or in numerical terms (point spread).  Sometimes the output even comes with an estimate of the uncertainty, for example in political polling where margin of error is often quoted. The existing methods clearly do have value, but this post concerns itself with two claims:

1. Prediction is not always ideal for what we really want to know
2. Prediction is often enhanced, sometimes materially by combining it with unsupervised learning techniques

Let start with the first premise, that prediction may not be the right technique in certain circumstances.

The output of a prediction methodology is often used as input to an optimization algorithm.  For example, predictions of stock prices are often used in portfolio optimization, prediction of outcomes of athletic contests are used in optimizing a betting portfolio, and results of election polling used to determine the choices made by political parties in supporting various candidates.  There are many powerful methods for optimization, and applying the predictive information obtained by these methods is often a straightforward process. However, in order to use them, it is required that one starts with a well-defined objective function to which one can apply optimization methods in order to maximize or minimize it.  

Herein lies the challenge.

In many situations it is unclear what defines a good objective function. Further, our attempts to create a proxy for an ill-defined objective function makes matters worse (for example, sometimes we choose a function that is easy to define and compute with, but that doesn’t make it good, it just makes it easy). Let’s consider a few examples:

1. We don’t know the objective function: Political parties often view themselves as optimizing aggregate societal well-being, but in fact it is very difficult for us to quantify societal well-being in terms of a single number.  For example, one might believe that per capita income is a reasonable proxy. On the other hand, it could be that inequality of incomes diminishes societal well-being even in situations where every person’s income is increased. While one’s views on this may be related to their political orientation – we simply don’t know the answer.  Similarly, airlines may optimize their dollar cost per passenger, resulting in less space per passenger and less flexibility in scheduling flights. It is easier mathematically to focus exclusively on cost, but it might be better in the long term to optimize the customer experience with the goal of driving revenue. Again, there is no clear answer. .
2. We disagree about the objective function: Suppose that we are trying to optimize health outcomes for individuals.  One person might feel that an objective function that maximizes expected lifespan is entirely appropriate. Such an objective function is easy to obtain mathematically and statistically.  On the other hand, another person, who likes beer, would not feel that an objective function that focuses entirely on expected lifespan is appropriate for him/her, since it might be the case that beer-drinking would lower (marginally) his or her expected lifespan.  The tradeoff of a potentially somewhat shorter lifespan versus the pleasure of drinking beer might very well be appropriate for that person.
3. We care most about minimizing very bad outcomes:  In many situations, it is not so important to us find optimal strategies as it is to ensure that nothing completely catastrophic occurs.  In financial portfolio management, if one is working with a client who is nearing retirement, it may be much more important to avoid significant losses than it is to optimize growth. Similarly, if one is treating patients suffering from heart disease, it is of much higher priority to avoid disastrous outcomes such as infection and/or death than to optimize for length of stay or to minimize the expenses.

In all these situations, the notion of prediction becomes significantly more difficult when the role of the objective function is unclear or debatable.  

Because we are not in a position to define an objective function, we cannot rely exclusively on optimization techniques to solve the problems that face us.  This means we need to take a step back and understand our data better so that we might guide ourselves to better outcomes.

This is where unsupervised learning comes in.

Unsupervised learning allows us to explore of various objective functions, find methods that permit the adaptation of an objective function to individual cases, and search for potentially catastrophic outcomes.  

These tasks cannot be resolved by methods whose outputs are a single number.  They instead require an output with which one can interact in addressing them, and therefore is equipped with more information and functionality than simple binary or numeric outputs. It is also vitally important that the methods we use let the data do the talking, because otherwise our natural inclinations are to verify what we already believe to be true, or to favor an objective function we have decided on, or to decide that we already know what all the relevant factors in an analysis are.

This is, in many ways, the underappreciated beauty in unsupervised approaches.

OK, what we have established so far is that:

1. Prediction needs a numerical objective function
2. For a variety of reasons, an objective function may be hard to come by
3. Unsupervised learning can help define the objective function by providing more insight into the structure of the data

So what are the  capabilities required of such unsupervised methods?

1. Defining and analyzing subpopulations of data sets: In analyzing the effect of various objective functions, it is critical to understand their effect on distinct subpopulations within the data.  For example, certain government policies may have widely different effects on various populations. It might be the case that certain governmental policy prescriptions provide an aggregate improvement for the population as a whole, but are disastrous for members of some subpopulations, and should therefore be rejected.  In many situations, the subpopulations or the taxonomy of the data set are not defined ahead of time, but need to be discovered. It is therefore important that the unsupervised method provide techniques for discovering subpopulations and taxonomies. This capability is very important for the situations identified earlier – namely where we don’t know or agree up on the objective function.
2. Location of “weak signals” in data: When we are focused on minimizing bad outcomes, it is often the case that those very  outcomes appear in past data as anomalous outcomes or outcomes which occur rarely (we call them weak signals), and then grow into stronger phenomena over time.  This kind of situation is not captured in many prediction methods, since the stronger signals tend to drown out the weaker signals in the output of these methods.  What is required is a methodology that performs a systematic kind of anomaly detection, and, is rich enough that it can include both strong signal and weak signal in one output.  Simple numerical methods cannot have this capability. In general, it requires a method that accommodates both analysis and search of the data set.
3. Unsupervised analysis over time: Of course, the temporal information about data sets plays a critical role in any kind of prediction.  It is often incorporated using algebraic regression methods, but for the kind of problems we are discussing, it is important to understand time dependent behavior in unsupervised analyses. For example, populations may increase or decrease over time in their proportion of the total data, they may split into smaller populations, and they may also merge. This kind of information is important in making any kind of predictions and optimizations based on the unsupervised information.

When we can deliver against these challenges, the performance of the prediction improves materially.

For example, we are working with a major manufacturer on a problem of particular value to them. They make very complicated widgets and failure rates are paramount. Every .01 percent change has tens of millions of dollars in bottom line impact. Their prediction capabilities had tapped out and no longer yielded valuable information. By employing unsupervised approaches, the company determined a key piece of information, namely that there were many different kinds of failure and those failures were not distributed evenly across their factories. This allowed them to take immediate steps to improve their failure rates.

So what are some techniques to create this one/two punch of unsupervised learning and supervised prediction?

There are many notions of unsupervised analysis, including clustering, principal component analysis, multidimensional scaling, and the topological data analysis (TDA) graph models.  

The TDA models have by far the richest functionality and are, unsurprisingly, what we use in our work. They include all the capabilities described above.  TDA begins with a similarity measure on a data set X, and then constructs a graph for X which acts as a similarity map or similarity model for it. Each node in the graph corresponds to a sub-collection of X.  Pairs of points which lie in the same node or in adjacent nodes are more similar to each other than pairs which lie in nodes far removed from each other in the graph structure. The graphical model can of course be visualized, but it has a great deal of other functionality.

• Segmentation: From the graph structure, one is able to construct decompositions of Xinto segments, each of which is coherent in the sense that includes only data points that are reasonably similar.  This can be done manually or automatically, based on graph theoretic ideas.
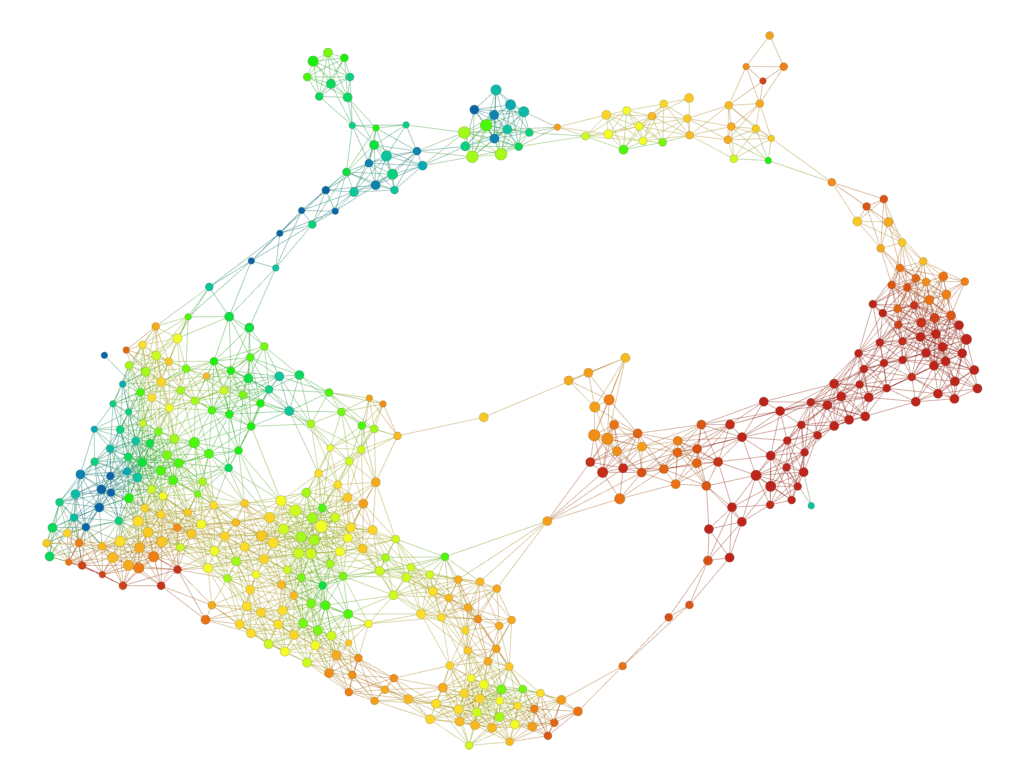
• Coloring by quantities or groups: Suppose that we have a data set, equipped with a particular quantity q we might be interested in, such as survival time in a biomedical data set or revenue in a financial data set.  Then we can attach a value to each node by forming the average of the values of q for all the data points in X in the group attached to the node. By assigning a color scale to the values of q, we obtain a coloring of the graph model, which yields a great deal of insight into the behavior of q.  Here’s an example.  The graph below is a model of a data set of roughly 200 responses to a survey that asked questions about various topics, including trust in societal institutions,  right/left political preference, and membership in various groups. It is colored by the answer (on a scale of one to ten) about the respondents’ right/left political preference, with low numbers (blue) corresponding to left preference and large numbers (red) to right preference.   
  
  
  Similarly, if one has a predefined group G within X, one can assign to each node v the percentage of points within the collection corresponding to v which also belong to G, and also color code that percentage.  Below is the same graph we saw above, but now colored by percentage of respondents who belong to a labor union (red is concentrated union membership).  
  
  
  This gives an understanding of the distribution of the group G within X, which can be very informative in designing objective functions. One can observe, for example, that the heavy concentrations of labor union members does not overlap with the darkest red regions obtained by coloring by right/left preference.  
• Anomalies and weak signal: TDA models have the ability to surface phenomena that have small extent and relatively small effect.  For instance, one might detect a very small group of people whose income is greater than others but whose profiles are similar to theirs.  Their income might not be very high relative to all the members of the data set, but the fact that they are higher than their “neighbors” in the model might be quite interesting.  Similarly, one might see that a small number of credit card transactions that appear different from previously observed transactions but that sufficiently similar to each other to invite additional scrutiny – indeed they may be group which might be growing in the future.
• Explaining phenomena: Given a group G within a data set X, it is important to understand what characterizes the group as distinct from the rest of X.  This can be formulated in terms of statistical tests to produce ordered lists of features in the data set that best differentiate between the group and the rest of the population.  This is another capability that is extremely useful in designing objective functions.

To summarize, it is fundamentally important to move from the idea of pure numerical or binary prediction to methods that permit one to have a better understanding of ones underlying data in order to design better objective functions and capture small and weak phenomena, that may eventually become very significant.  TDA provides a methodology that is very well suited to these requirements.