Determining sample sizes is a challenging undertaking. For simplicity, I’ve limited this picture to the one of the most common testing situation: testing for differences in means. Some assumptions have been made (for example, normality and equal sample sizes). Additionally, the formulas shown are for one-tailed tests. Usually, a small tweak (e.g. replacing Zα by Zα/2) is all that’s required for two-tailed tests.
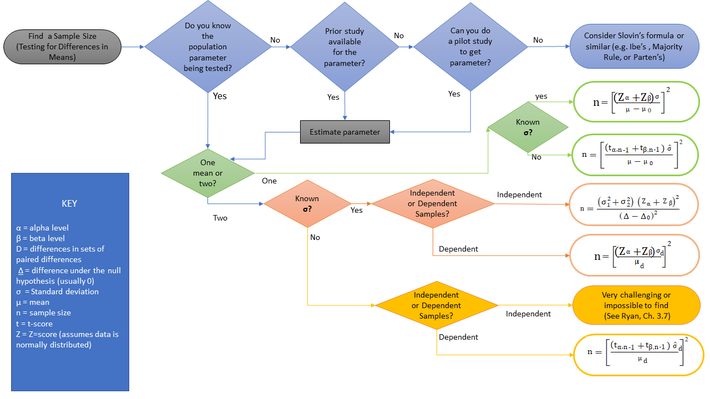
Click on the picture to zoom in
The picture shows the traditional (frequentist) route for determining sample size. Another possible route is to use Bayesian methods. Although becoming more popular, none of the major software programs include those methods and–unlike the frequentist route—no standard Bayesian methods exist for determining sample size. If you’re interested in Bayesian methods, refer to Chapter 13 in Chow, et al, 2008.
Further Information:
References
Chow et. al (2017). Sample Size Calculations in Clinical Research. CRC Press
Ryan, T. (2013). Sample Size Determination and Power. Wiley.
DSC Resources
- Free Book and Resources for DSC Members
- New Perspectives on Statistical Distributions and Deep Learning
- Time series, Growth Modeling and Data Science Wizardy
- Statistical Concepts Explained in Simple English
- Machine Learning Concepts Explained in One Picture
- Comprehensive Repository of Data Science and ML Resources
- Advanced Machine Learning with Basic Excel
- Difference between ML, Data Science, AI, Deep Learning, and Statistics
- Selected Business Analytics, Data Science and ML articles
- How to Automatically Determine the Number of Clusters in your Data
- Hire a Data Scientist | Search DSC | Find a Job
- Post a Blog | Forum Questions
