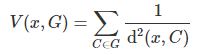I describe here an interesting and intuitive clustering algorithm (that can be used for data reduction as well) offering several advantages, over traditional classifiers:
- More robust against outliers and erroneous data
- Executing much faster
- Generalizing well known algorithms
You don’t need to know K-NN to understand this article — but click here if you want to learn more about it. You don’t need a background in statistical science either.
Let’s describe this new algorithm and its various components, in simple English
General Framework
We are dealing here with a supervised learning problem, and more specifically, clustering (also called supervised classification.). In particular, we want to assign a class label to a new observation that does not belong to the training set. Instead of checking out individual points (the nearest neighbors) and using a majority (voting) rule to assign the new observation to a cluster based on nearest neighbor counts, we are checking out cliques of points, and focus on the nearest cliques rather than on the nearest points.
Cliques and Clique Density
The cliques considered here are defined by circles (in two dimensions) or spheres (in three dimensions.) In the most basic version, we have one clique for each cluster, and the clique is defined as the smallest circle containing a pre-specified proportion p of the points from the cluster in question. If the clusters are well separated, we can even use p = 1. We define the density of a clique as the number of points per unit area. In general, we want to build cliques with high density.
Ideally, we want each cluster in the training set to be covered by a small number of (possibly slightly overlapping) cliques, each one having a high density. Also, as a general rule, a training set point can only belong to one clique, and (ideally) to only one cluster. But the circles associated with two cliques are allowed to overlap.
Classification Rule, Computational Complexity, Memory Requirements
Once we have built a set of cliques for each cluster, the classification rule is straightforward. Building these cliques is the complicated pre-processing step, but as discussed in the last section, we only need a rough approximation. The classification rule is as follows:
- 1-NC algorithm: Assign the new observation to the cluster attached to the nearest clique
- K-NC algorithm: Assign the new observation to the cluster that has the largest number of cliques, among the K cliques closest to the observation in question (majority vote).
Note that if cliques consist of a single point, then K-NN and K-NC algorithms are identical. Also note that computing the distance between a point and a clique is straightforward, because cliques are circular. You just need to know the center of the circle in question, and its radius.
Finally, to assign a new observation to a cluster, one only has to check all the cliques, rather than all the points. Thus the K-NC algorithm is v times faster than K-NN, where v is number of points in the training set, divided by the number of cliques across all clusters. In practice, we have far fewer cliques than we have points in the training set, so v can be large, when dealing with very big training sets. Especially if there is not too much overlap among the cliques.
In short, the cliques summarize the training set data: we can discard all the data and only keep the cliques (with their center, radius, density, and cluster label), once these cliques have been computed. This also saves a lot of memory, and in itself can be used as a data reduction technique.
Cliques Building and Smallest-Circle-Problem
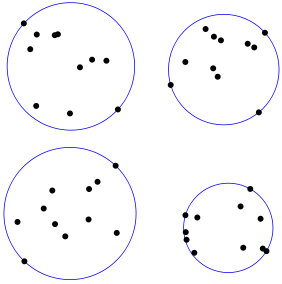
This concept could prove useful when building the clique system. The smallest-circle-problem (click here for details) consists of computing the smallest circle that contains all points in a given region. It is illustrated in Figure 1 below.
Figure 1: Cliques computed based on the Smallest-Circle-Problem
One would think that such cliques have maximum density, a desirable. property. Several very efficient algorithms are available to solve this problem. Some even allow you to attach a weight to each point.
Gravitational Field Generated by Clusters
You can skip this section. It has been included for those interested in further improvements of the K-NC algorithm, as well as improving standard algorithms such as K-NN, Also, it highlights the fact that the square of the distance, could be a better metric than raw distance (from a modeling point of view) when averaging proximity among points, just like many physical laws involve the square of the distance between two objects, rather than the distance itself. You can look at a classification problem the same way that you would at the gravitation law: which cluster is going to “attract” a new observation (in the context of classification), versus which celestial body is going to attract and adsorb a meteoroid (in the context of celestial physics.) You would think that in both cases, similar laws apply.
For each point x (typically, a new point that we want to classify) and cluster G, the potential V(x, G) is defined as follows:
where the sum is over all cliques in G. A better definition might be to take the sum only over the k nearest cliques in G, for a pre-specified value of k. A potential classification rule consists of assigning a point x to the group G that maximizes V(x, G).
A final improvement consists in attaching a weight to each term in the above sum: the weight being the density of the corresponding clique. Note that if cliques (their circles) significantly overlap, this should be addressed in the definition of the potential V. As a general rule, a training set point can only belong to one clique, and (ideally) to only one cluster.
Building an Efficient Clique System
This data pre-processing step is the more complicated step. However, easy-to-obtain approximate solutions work well. After all, even if each point is a clique (the K-NN particular case) we get very good results.
Different approaches are possible:
- Start with one clique per training set point, and iteratively merge the cliques
- Start with one clique per cluster, based on the smallest-circle-problem described earlier. Then shrink it and move the center till it contains a proportion p of the training set points, for the cluster in question, and the density of the clique is maximum (or close enough to maximum.) Repeat the operation for the remaining points in the cluster in question. Maybe choose p = 30% assuming each cluster has a circular core consisting of at least 30% of its points.
- Start with a pre-specified number of random cliques (random radius, random center, possibly corresponding to a point randomly selected in the training set.) in each cluster. Adjust the centers and radii one clique at a time to optimize some density-related criterion described below. Also, it would be a good idea to use a birth and death process to eliminate some cliques and create new ones over time.
The aim is to obtain as few cliques as possible, covering the entire training set without too much overlapping. Each clique must have a high density, and must contain more than (say) 1% of the training set points for the cluster in question. We could add another constraint: each clique must have at least two points.
Non-Circular Cliques
It would be interesting to test whether the shape of the clique matters. As long as we have sufficiently many cliques, the shape probably does not matter (this should be tested), and thus a circle — because it leads to considerably simplified computations when measuring the distance between a clique and a point — is ideal. Note that if a point is inside a clique (inside its circle) then the distance between the clique and the point is zero. We should test whether this rule leads to more robustness against outliers or erroneous data.
Source Code
I hope to come up soon with a piece of code for the K-NC classifier, and especially, to build clique systems that work well. Obviously this algorithm is better than K-NN in the sense that it is a generalization (and it can also be used for data reduction) but it would be interested to test what kind of cliques (small or big ones) provide the best result based on cross-validations, and how big the improvement is.
In the meanwhile, I encourage the reader to design an implementation, maybe in Python. This would be a great data science project. I will publish and feature these solutions, provide an endorsement to the author (for instance, on LinkedIn) and send him/her a signed copy of my Wiley book.
Potential Enhancements, Data Reduction, and Conclusions
Potential improvements to our methodology include:
- Using density in addition to proximity, putting more emphasis on dense cliques when assigning a new observation to a cluster
- Allowing training set points to belong to multiple cliques within the same cluster
- Allowing training set points to belong to multiple clusters
- Testing cliques that are made up of closest neighbors
- Reducing the overlap among cliques
Also, we need to test this new algorithm, and see when it performs best, depending on how cliques are created. Is K-NC almost equivalent to K-NN, provided a different K is used in each case? Even if they are equivalent, K-NC has one great benefit: it can be used for data reduction, in a way that is different from traditional data reduction techniques. Traditional data reduction techniques such as PCA try to project the data set onto a space that has a lower dimension. The clique structure produced by K-NC is the result of a data reduction technique that does not perform dimension reduction nor projections, but instead, performs something akin to data compaction or data compression or entropy reduction, in the same original space.
Another benefit is the fact that K-NC, thanks to its pre-processing step to build the clique structure, runs much faster than K-NN. It is also more intuitive, as it is based on the intuitive concept that each cluster is made up of sub-clusters: the cliques. It is indeed similar to model fitting with stochastic point processes representing cluster structures, such as Neyman-Scott cluster processes.
Finally, in many cases, one way to improve a classifier is by re-scaling or transforming the data, for instance using a logarithmic scale. Most classifiers are scale-dependent, and we are now working on developing scale-invariant classifiers, just like we introduced a scale-invariant variance a while back.
To access all my data science articles, click here.
DSC Resources
- Services: Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Contributors: Post a Blog | Ask a Question
- Follow us: @DataScienceCtrl | @AnalyticBridge
Popular Articles