Fermat’s last conjecture has puzzled mathematicians for 300 years, and was eventually proved only recently. In this note, I propose a generalization, that could actually lead to a much simpler proof and a more powerful result with broader applications, including to solve numerous similar equations. As usual, my research involves a significant amount of computations and experimental math, as an exploratory step before stating new conjectures, and eventually trying to prove them. The methodology is very similar to that used in data science, involving the following steps:
- Identify and process the data. Here the data set consists of all real numbers; it is infinite, which brings its own challenges. On the plus side, the data is public and accessible to everyone, though very powerful computation techniques are required, usually involving a distributed architecture.
- Data cleaning: in this case, inaccuracies are caused by no using enough precision; the solution consists of finding better / faster algorithms for your computations, and sometimes having to work with exact arithmetic, using Bignum libraries.
- Sample data and perform exploratory analysis to identify patterns. Formulate hypotheses. Perform statistical tests to validate (or not) these hypotheses. Then formulate conjectures based on this analysis.
- Build models (about how your numbers seem to behave) and focus on models offering the best fit. Perform simulations based on your model, see if your numbers agree with your simulations, by testing on a much larger set of numbers. Discard conjectures that do not pass these tests.
- Formally prove or disprove retained conjectures, when possible. Then write a conclusion if possible: in this case, a new, major mathematical theorem, showing potential applications. This last step is similar to data scientists presenting the main insights of their analysis, to a layman audience.
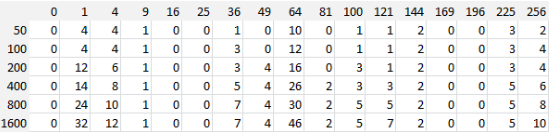
See full article for explanations about this table (representing the number of solutions)
The motivation in this article is two-fold:
- Presenting a new path that can lead to new interesting results and theoretical research in mathematics (yet my writing style and content is accessible to the layman).
- Offering data scientists and machine learning / AI practitioners (including newbies) an interesting framework to test their programming, discovery and analysis skills, using a huge (infinite) data set that has been available to everyone since the beginning of times, and applied to a fascinating problem.
Read full article here. For more math-oriented articles, visit this page (check the math section), or download my books, available here.
