One of my most memorable experiences during my college years was having an English professor who spoke entirely in complete sentences.There were no spoken sentence fragments, dangling thoughts or misuse of adjectives, verbs or nouns. When I first met him, I was stunned at his level of commitment to this principle. I often wondered how challenging this must be for him and whether or not the journey had instances where a thought started and had to be gracefully abandoned into a mundane compromise of a sentence. It was probably also difficult to not have the verbal equivalent of a delete key. How was this possible, if not rehearsed?
I immediately started considering what level of commitment it would take to do the same in mathematics. Can one speak in complete mathematical sentences? What are the rules for thinking in math? Do the same rules apply for writing in mathematics? Furthermore, what are the rules for writing in mathematics? If learning math is like learning a foreign language because of the various symbols and algorithmic rules, are there opportunities that teachers can leverage that will allow students to have greater access in communicating their thinking and ideas in mathematics? One fact is certain, the way that mathematics is currently taught is often lacking context and motivation, and alienates students. Mathematicians need to allow students various entry points to the content. Simply providing an equation, formula, graph, illustration or text without clear explanations, furthers the myth that mathematics is inaccessible to the masses.
First Writing in Mathematics
For most students, the first writing experience in mathematics typically involves the writing of numbers. Tally marks provide a nice transition to the notion of keeping track-of and summarizing the concept of ‘number’. Then, there is often times a leap to the algorithmic thinking of addition, subtraction and multiplication solely represented as setting up the problem in a traditional format. After working with students of all ages, it has become abundantly clear that this approach endorses algorithm thinking in lieu of conceptual understanding. In fact, having students write about the process of using the algorithms and describing how they work does more for their conceptual understanding than just solving problems.
Examples of math sentences at an early age include: 1+2=3, 5 x 4=20 and 12–7=5. In its simplest form, math sentences reflect math facts, uses simple operators like {+, — , x} and include at least two operands.More importantly, having students write to describe what they are doing holds much more value. In addition, changing the problem slightly by making one of the operands a question mark opens up their thinking to include multiple answers. For example: ?- 4 = 17, 50 – ? =23 or ? x ?= 34 all promote deeper thinking tasks to write about. Beyond this notion of mathematical sentences lies a deeper notion of mathematical thinking. Therefore, it’s less about sentence structure and rather how we can develop the ability of students to think more broadly about problem solving.
Mathematical Problem Types
Although word problems in mathematics can be introduced in elementary grades, middle grades tend to spend quite some time in developing students’ skills on these types of problems. These skills can best be described as the ability to :
- Identify important information in word problems
- Determine variables and constants
- Understand what the problem is asking
- Identify relationships between variables
- Construct an equation that would lead to a solution
- Solve the given algebraic equation
These are all very important skills to develop and hone. However, these skills also underscore the notion of a single approach to problem-solving which leads to a single solution. This is contrary to how mathematicians approach real-world problem-solving. For mathematicians, a considerable amount of time is spent writing and reflecting on multiple ways to get to a variety of solutions based on what’s being optimized. Asking the right questions goes a long way toward finding a solution. Using this approach results in multiple solutions based on many of the decisions that must be made about the problem-solving approach. Given these facts, here is an illustration of how students spend their time writing and thinking about mathematics versus how mathematicians do the same.

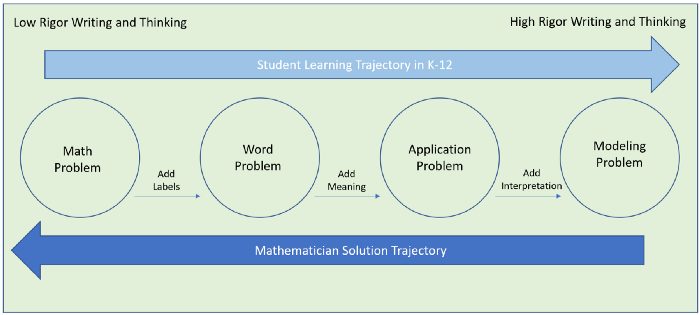
Rigor in mathematical writing and thinking increases from left to right. Note that some students have K-12 experiences that focus on obtaining a single solution and never move beyond the word problem stage. Whereas, mathematicians approach problem solving by spending considerable time detailing and describing possible mathematical models, often leading to multiple solutions, effectively communicate their solutions and publish their work for others to review. Adapted from SIAM “Guidelines for Assessment & Instruction in Mathematical Modeling Education”
Application problems are typically tied to a specific field or context and might contain real-world data for students. However, the problems are still closed in the sense that many of the decisions, variables and values have already been pre-determined. It may take the form of a pre-determined equation of how a ball behaves when thrown or dropped and use real-world measurements to test the model. Mathematical modeling problems are different in that, most of the decision making of how to construct the model, determine which variables to use, determine which data to collect, and choosing what is important are left up to the student. The student quickly understands that there may be multiple solutions and that the quality of the solution will be important. Questions begin to emerge about the solution and approach, such as: how close is my solution to the performance of the phenomena? Can I use this model to make predictions about future or past behavior? Can this model solve other similar phenomena-based problems? The writing and thinking that is involved in modeling problems far exceed the writing and thinking involved in applying an algorithm to solve a computational problem.


Photo by Patrick Amoy on Unsplash
Coding as Writing in Mathematics
If writing is an expression of thinking, then it’s time to allow every student of mathematics to learn how to write code. Coding is now considered to be an essential skill in developing algorithmic thinking. It is not just suitable for engineering, technology or math majors, it is an essential skill for all students to learn problem-solving. When I went to high school, coding was taught in my math courses and if we were lucky, we would have a separate computer class to learn various languages. Simply put, you can’t fully grasp some mathematical concepts without experimentation and investigation. Coding allows for this. Not allowing students to code in mathematics is akin to teaching art without a canvas and brushes or teaching writing without a pen. Coding should be viewed as a tool for expressing mathematical ideas. It is a form of thinking and writing that is essential for understanding mathematics.
Writing Tools
The gold standard for typesetting in mathematics is LaTeX. It is a markup language similar to html that’s used by math researchers across the globe. When it comes to the tools that are available for writing mathematics, there is a huge challenge. Many of the applications that are available, including TeX and LaTeX, are simply inaccessible to teachers and students. Microsoft’s Equation Editor within the Word application is cumbersome for students to search for and use the various operators and symbols to communicate their ideas. Most math writing applications have a significant learning curve for both teachers and students. Part of the challenge lies in the fact that math has very complicated text requirements. A writing tool for mathematics will need to allow for creating graphs, tables, special characters, special operators and formatted text.
Toward the goal of making writing in mathematics more accessible, many companies are following what was initially proposed by Wolfram’s Mathematica many years ago. That is, they created a tool which allowed students to collect their thoughts, graphs, scripts, algorithms and formatted text into a single document called a notebook within the application. Several other companies are following suit. Examples include Jupyter Notebook for Python scripts, Matlab Live Editor from MathWorks, Scientific Notebook by MacKichan Software and R-Studio’s R-Markdown. Many of these programs also allow for embedding TeX or LaTeX scripting as part of their feature set.
Conclusion
I still can’t do what my college English professor did many years ago. But with computers, I can think more broadly about problem solving in a variety of domains. It’s time for a change! Let’s make coding a requirement in every math course for students. We can begin by supporting university teacher preparation programs in developing a coding curriculum that is accessible for all teachers. Teachers need to develop the skill, will and capacity to learn the relevance and importance of coding.
Having taught History of Mathematics courses at the university level, what is astonishing to me is the organic nature of the development of mathematics. The complex mathematical rules that govern the universe were developed many centuries ago from a simple need to describe the concept of a number. It was only through an iterative process of experimentation, modeling, trial and error, approximation and documentation that we as humanity were able to make the many leaps in science, technology engineering and mathematics. Computing technology now provides us with tools which can expedite these experiences and learnings. We should embrace these tools and take mathematics to a new level by empowering students to write about their experiences. Let’s also not forget the power of the incredible, easily accessible technology known as pen and paper.
