A classic classical discontinuity: “Leaping the Chasm” (1886) by Ashley Bennett, son of photographer Henry Hamilton Bennett, jumping to “Stand Rock”. See www.wisconsinhistory.org
I am happy to announce that today I added 2 new chapters to Bayesuvius (my free, open source book on Bayesian Networks). The titles of the 2 new chapters are
- Difference-in-Differences (DID)
- Regression Discontinuity Design (RDD)
Bayesuvius now has 50 chapters and 285 pages.
DID and RDD are two applications of Rubin’s theory of Potential Outcomes (PO). In case you don’t know what PO theory is, Bayesuvius has a chapter on PO theory too.
DID is a very old and venerable method first used in 1854 by John Snow to do causal epidemiology. In 1854, Snow published a report arguing that cholera was being transmitted in London by sewage-polluted drinking water, rather than, as many believed at the time, by air (via fetid vapors called miasmas).
RDD is a method in which a treatment is influenced by the experimenter via a confounding variable X. X exerts no influence below a threshold value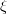 
, but exerts a large influence for X above 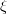. This discontinuous behavior in X is reflected by a discontinuity 
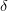in the outcome of the treatment. By measuring 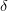, we can measure the causal effect of the treatment itself. For example, the treatment might be whether or not an individual is admitted to Harvard Univ., the treatment outcome might be how much money the individual earns for the first 20 years after graduating from Harvard, and X might be his SAT scores. We assume Harvard only admits students with an SAT score higher than .
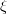Perhaps the theory of RDD can be applied to classical and quantum detectors in which a discontinuity is observed (for example, in a Geiger counter or a photodetector). Classical detectors are designed to detect classical behavior and quantum detectors are designed to detect quantum behaviors. Quantum detectors are particularly sensitive because a quantum wave-function is so easily corrupted by external influences . A quantum detector might be able to detect quantum events (like an electron jumping from one energy level of an atom to another) that a classical detector might fail to detect.
