
No, I am not a flat-earther. Quite the contrary, the ideas suggested here assume advanced scientific knowledge, such as quantum physics. The famous Cambridge-based physicist Stephen Hawking suggested that we may live in a universe with 11 dimensions. What I discuss here is not conflicting with that statement, as we shall see.
It all started one night, going outside for a walk. I have a problem with one of my eyes: a difficulty transitioning from dark to bright light. During the unusually long transition period, I experienced vision flickering in that eye. It is almost like watching a video, if the screen refreshing rate was 10 times per second, rather than 20: images do not appear in a continuum, and the eye notices the individual frames flickering. I then read that dogs and cats have a much sharper vision, and when watching a video made for human beings, they see the individual frames because their brain (as far as image processing is concerned) have a much higher refresh frequency, see here. Actually, there are some programs and TV sets designed specifically for dogs, with a higher refresh rate to avoid the problem.
Then I started to wonder if some other creatures have an even higher refresh rate for images. And from that point on, I started to ponder the following question: what if the reality itself consists of frames, not a time continuum, but discrete snapshots occurring with an incredibly high, yet finite frequency. This is like saying that infinity or continuum does not exist in nature, but is only an artificial construct or a perception of the brain (human or dog), or in other words, something similar to an optical illusion.
The next step was to ask the same question about distances and space. Is there only a finite number of locations in the universe, an incredibly gigantic number, yet finite. In other words, when we move from point A to B, do we move by tiny increments or jumps, from one location to the next one, separated by distances far smaller than the distance between two protons in an atom. To be more precise, a distance possibly equal to Planck’s length. A result in theoretical physics is that it is impossible to measure distances smaller than that. So not only we could potentially move by discrete jumps in space, but also discrete jumps in time, and possibly discrete jumps in other dimensions of the universe, that we are not aware of. An implication is that matter is not continuously dense, and even ourselves, human beings, are mostly made of void.
What about the void in the universe, representing the vast majority of the universe? Does it count as a part of the universe? One might ask the same question about time: is it mostly made of void? That is, time that no one ever access at any given moment – time that in short, for all purposes, does not exist. In other words, what is between the discrete time instances that we live in? Of course, these voids evolve in all the dimensions that we live in, be it space, time, or anything else.
Stephen Hawking also suggested that the extra dimensions of the universe, besides space and time, may be very thin and thus unnoticed by human beings, just like the ecliptic plane is almost flat (2-D) though it can’t possibly be perfectly flat. In fact, the North and South pole of Earth are above and below the theoretical ecliptic plane (unless you are a flat-earther but even then, mountains have some height). Thus that plane can’t really be perfectly flat; it can’t be a plane, it is 3-D (at least). What I am saying here is that the yet unknown extra dimensions of the universe, could be as “flat” as the ecliptic plane.
You may wonder why the title of my article is about a universe with fewer than three dimensions, when I keep adding more and more, and I am not contesting Hawkins’s statement about the eleven dimensions of the universe. But before providing an explanation, let’s ponder one more point. The human-made laws of the universe governed by differential equations, although incredibly precise, are never exactly correct. This could explain why quantum physics and the theory of relativity do not agree, and no one has yet found a unifying theory. Even in mathematics, the claim that real numbers form a continuum comes with some challenge: the vast majority of numbers are non-computable; in short, not accessible, as if they did not exist, as if they were a construct of the human brain. See here. Some may argue that the universe is a combination of both discrete and continuous systems, as opposed to being either entirely discrete, or entirely continuous.
Now let’s discuss the number of dimensions of the universe. No one will contest the chaotic nature of the place where we live – our universe. It is as if we live in a fractal universe, one in which each dimension is actually a fractal dimension. The dimension of a 2-D fractal, plotted on a 2-D screen, is actually less than two. It has what is called an Hausdorff dimension, see here. The fractal seems to fill the space continuously, it is indeed dense in the space (using the mathematical definition of the word dense). But you can’t see to the naked eye that is is peppered with microscopic holes, so many of them indeed, that in reality, it consists almost exclusively of these holes (or void). If you sum up all the Hausdorff dimensions of the universe, and each one is actually a dimension “less than one”, you could possibly end up with a universe with fewer than three dimensions.
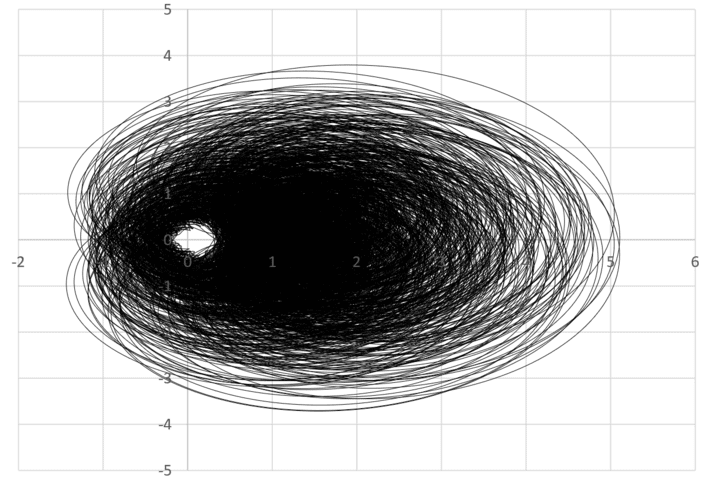
I illustrate the concept of “empty space” or “void” with the picture below, featuring a particular case of the one-dimensional orbit of the Riemann zeta function. I say “one dimensional” because it is a curve in a 2-D space; just like a straight line, it is supposed to have one dimension. Yet, it seems to completely fill an entire portion of the plane, and one might be tempted to say that it has two dimensions. But if you measure its area, it is zero. The vast majority of the potential locations will never ever be visited by the orbit even in its densest, darkest parts. What if that orbit itself, the one-dimensional curve, was filled with plenty of holes (corresponding to the aforementioned uncomputable numbers on the real line)? The time parameter used to show the orbit is continuous, but then maybe not. Indeed, I computed the orbit using tiny increments, a lot of them yet a finite number of them, and all computable ones. And yet, visually it looks continuous. Also, in the picture below, there are only finitely many pixels on your screen when you look at the orbit. And I could not possibly have computed all the locations on my laptop even if theoretically feasible: I had to use finitely many computable increments, otherwise it would have needed more electrical power than the total amount of energy available in the universe, and an infinite amount of time even with a computer processing data at a speed far, far faster than the speed of light. What I mean here (if this orbit was supposed to represent a natural feature of the universe) is that not only its dimension is smaller than two despite appearances, but it could even be smaller than one. Flat-earthers would never ever have imagined such a reduction of dimensions!
To receive a weekly digest of our new articles, subscribe to our newsletter, here.
About the author: Vincent Granville is a data science pioneer, mathematician, book author (Wiley), patent owner, former post-doc at Cambridge University, former VC-funded executive, with 20+ years of corporate experience including CNET, NBC, Visa, Wells Fargo, Microsoft, eBay. Vincent is also a self-publisher at DataShaping.com, and founded and co-founded a few start-ups, including one with a successful exit (Data Science Central acquired by Tech Target). You can access Vincent’s articles and books, here. A selection of the most recent ones can be found on vgranville.com.
