Bias Variance Trade Off

Deep Learning is a highly empirical domain which majorly focusses on fine-tuning the various parameters. The choice of these parameters defines the accuracy of the model. So, it becomes important to choose such parameters wisely. Choosing the parameters based on intuition might not work every time which can degrade the performance of the model drastically. Also, a considerable amount of time and effort will go in vain while selecting the values of parameters based on intuition. So, the methodological approach should be followed to select the optimal values of parameters to maximize the accuracy of the model.

There is an n number of parameters which needs to be fine-tuned. Some of them are:

1. Number of layers
2. Number of hidden units
3. Choice of activation function such as sigmoid, tanh or rectified linear unit
4. Choice of optimization algorithms such as Gradient Descent, Adam optimization.
5. Regularization Techniques such as L2 regularization or L1 regularization
6. Network architecture such as Recurrent Neural Network(RNN), Convolutional Neural Network(CNN)
7. Collect more data.

Before deep diving directly into bias-variance trade-off, let us discuss a systematic approach to handle the Machine Learning problem.

The very first step to handle the machine learning problem is:

1. Set the correct distribution of train set, cross-validation or development set, and test set.
2. Select the correct evaluation metric depending on the problem statement.

Let’s talk about above-mentioned points in detail:

Data set is divided into train set, cross-validation set often called as development sets and test set. Generally, the ratio of 60-20-20 is followed i.e. 60% of data is used to train the model, 20% data for cross-validating the model to fine tune the parameters and 20% data to test the accuracy of the model on unbiased data set. One most important thing to keep in mind here is not to follow the general rule blindly. The distribution of data into train set, development set, and test set majorly depend on the size of data. For instance, if observations in the data set are as high as 1000000. Then 90-5-5 ratio or even 98-1-1 ratio works far better than the usual 60-20-20 rule. This is because all deep learning models have a hunger for data. Using 60-20-20 distribution in such a scenario would waste the large chunk of data which could be utilized for training the model. On the other hand, if the size of the data set is as small as 10000, 60-20-20 or 80-10-10 will work far better than 90-5-5 because the size of the data set is small. The key point to notice here is that we need at least 10% of the data to fine-tune the parameters of the model in this case. If the size of the cross-validation data set is too small then, it is likely that the model will overfit to cross-validation data set and hence will fail to generalize over test data.

Along with the division of data into train/dev/test set, another important parameter to be considered is “Development set or Cross-validation set and test set should come from the same distributions.”More importantly, Development set/Cross Validation set and Test set should reflect the real-world data which is expected to be seen by model.There are some applications where Dev sets/Test sets don’t come from some distributions. In those cases, there are a different set of methods for bias variance trade off. However, that topic is out of context for this blog post.

Selecting the correct evaluation metric is one of most important parameters in solving any deep learning problem which majorly depends on type of problem at hand and domain knowledge. The best practice is to select single evaluation metric. This practice can speed up the process of cross-validating the model and allows to experiment with different approaches for fine tuning the parameters. However, there are certain applications where one evaluation metric is not sufficient to measure the performance of the model. In those cases, it is recommended to select one optimizing metric and another satisficing metric. Let’s take the example of speech recognition to understand the concept of optimizing and satisficing metric. In speech recognition model, “accuracy” can be optimizing metric and “time required to train the model can be satisficing metric” can act as satisficing metric that means goal is to maximize the accuracy while satisfying the condition that time required to train the model must be less than 1min.

Prediction error can be broken down into three categories Bias, Variance and Irreducible error. Let’s talk about Bias and Variance to understand the Bias Variance tradeoff.

1. Bias:

Bias in simplest terms can be defined as “Assumptions made on the form of model which makes the learning of the model easier.”Let’s talk about the linear regression model which falls into the category of High Bias model. The linear Regression model is a parametric model because the shape of the model is assumed to be linear irrespective of the distribution of data. Since the form of the model is assumed to be linear, it might happen that model doesn’t fit the data well which results into underfitting. Generally, high bias models are linear/parametric models such as linear regression, linear discriminant analysis, logistic regression.

 2. Variance:

Variance can be defined as the “amount by which the estimate of target function will change if different training data was used”. Let’s take the instance of decision tree to understand the high variance model. The decision tree with a large number of nodes is likely to overfit the training data because with the increasing number of nodes model is specifically tuned to training data. It makes it difficult for the model to generalize on the other data. High Variance models include non-linear or non-parametric algorithms such as Decision Trees, K- nearest neighbors and Support Vector Machines.

High Bias leads to underfitting model and High Variance leads to overfitting as shown in the figure –

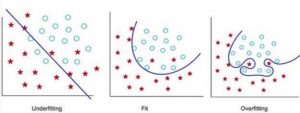
Here’s the basic approach to solve the Machine Learning problem. Let’s understand each of below step in detail.

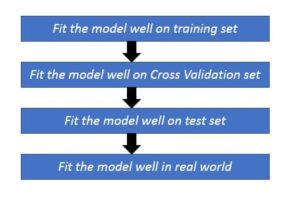
Once the data is divided into Train, Development and Tests sets as discussed in the article earlier. The next step is to fit the model on the training set and calculate the training error and the next step is to fit the model on cross validation set and calculate CV error and so on….

The first step is to check the training accuracy of model. Training accuracy of model tells us that “How good the model fits on training data i.e. it gives information about the bias of model.” Now, the question arises What is baseline accuracy? In applications, such as speech recognition, computer vision, medical record monitoring accuracy of model is measured with respect to human performance or Bayes optimal error as shown in figure.

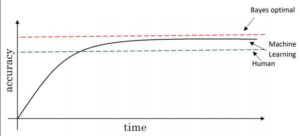
Bayes Optimal Error is defined as the lowest possible error for any classifier which is analogous to irreducible error.  Bayes Optimal Error is generally used as baseline accuracy for the problems where Machine Learning has significantly surpassed the human level performance. Some examples include Online Advertising, recommendation systems, Loan Approval where there is a lot of structured data should be analyzed. In applications, such as speech recognition, computer vision training accuracy is measured with respect to human performance.

Let’s take an example of Speech Recognition model to understand this concept. Training error of model came out to be 15% whereas human error on the same given task is 1%. This means model is not fitting well on training data itself i.e. “High Bias.”  The following ideas should be tried to approach High Bias problem.

1. Train a bigger model i.e. more number of hidden layers or more number of hidden units.
2. Train model for longer time.
3. Better choice optimization algorithms such as Gradient Descent, RMS Prop, Adam optimization algorithm.
4. Neural Network Architecture such as RNN or CNN.

Let’s take an instance of another speech recognition model. Training error for that model is 2% and human error is 1%. In this case, our model performance is good as it is nearly equal to human error. Hence, there is no “High Bias” problem. Here, Dev set/Cross Validation error is 10%. Since there is huge difference between training error and dev set error, it can be concluded that Model is suffering from “High Variance” Problem. This means the model is overfitted to training data and is not able to generalize well on the data which it has never seen before. Following ideas can be implemented to handle High Variance problem.

1. Try Regularization techniques such as L2 regularization or L1 regularization.
2. Fine tuning of hyper parameters.
3. Try to get more data.

After resolving high bias and high variance problem, the accuracy of model is checked on unbiased data set i.e. test set. If there is significant difference between Development Set error and Test set error then, there might be possibility of overfitting of model on development set. Getting a bigger development set generally works in such cases.

To generalize the conclusion drawn from the blog post, significant difference between human performance/bayes optimal error and training error signifies “High Bias” problem whereas the gap between training error and development set/ cross validation set error signifies “HighVariance” problem. Different methods should be used to deal with High Bias or High Variance problems rather than experimenting based on intuition.