I introduce here a family of very peculiar statistical distributions governed by two parameters: p, a real number in [0, 1], and b, an integer > 1.
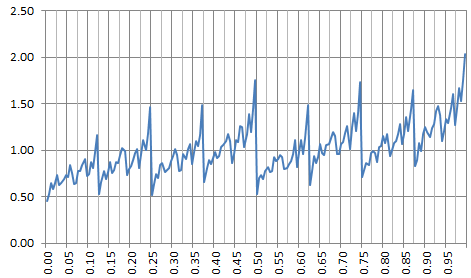
Potential applications are found in cryptography, Fintech (stock market modeling), Bitcoin, number theory, random number generation, benchmarking statistical tests (see here) and even gaming (see here.) However, the most interesting application is probably to gain insights about how non-normal numbers look like, especially their chaotic nature. It is a fundamental tool to help solve one of the most intriguing mathematical conjectures of all times (yet unsolved): are the digits of standard constants such as Pi or SQRT(2) uniformly distributed or not? For instance, when b = 2, any departure from p = 0.5 (a normal seed) results in a strong discontinuity for f(x) at x = 0.5. If you look at the above chart, f(0) = f(1/2) = f(1) regardless of p, but discontinuities are masking this fact.
