If X(1), X(2), …, X(n) are independent random variables, not necessarily with the same distribution, what is the variance of Z = X(1) X(2) … X(n)? It turns out that the computation is very simple:
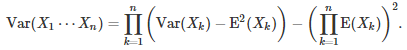
In particular, if all the expectations are zero, then the variance of the product is equal to the product of the variances. See here for details.
A More Complex System
Even more surprising, if
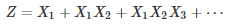
and all the X(k)’s are independent and have the same distribution, then we have
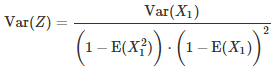
The proof is more difficult in this case, and can be found here. Note that the terms in the infinite sum for Z are correlated. Interestingly, in this case, Z has a geometric distribution of parameter of parameter 1 – p if and only if the X(k)’s have a Bernouilli distribution of parameter p. Also, Z has a uniform distribution on [-1, 1] if and only if the X(k)’s have the following distribution: P( X(k) = -0.5 ) = 0.5 = P( X(k) = 0.5 ). The proof can be found here. If you slightly change the distribution of X(k), to say P( X(k) = -0.5) = 0.25 and P( X(k) = 0.5 ) = 0.75, then Z has a singular, very wild distribution on [-1, 1]. Its percentile distribution is pictured below.
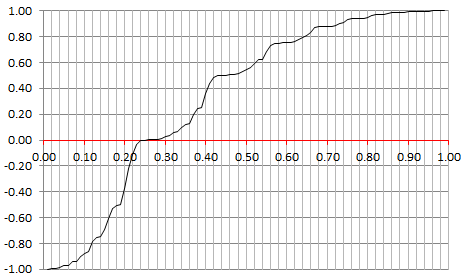The details can be found in the same article, including the connection to the binary digits of a (random) number in the base-2 numeration system.
