Why Machine Learning Doesn’t Work Well for Some Problems?
Shahab Sheikh-Bahaei, Ph.D.*
Principal Data Scientist
Intertrust Technologies.
Introduction
Machine Learning (ML) is closely related to computational statistics which focuses on prediction-making through the use of computers. ML is a modern approach to an old problem: predictive inference. It makes an inference from “feature” space to “outcome/target” space. In order to work properly, an ML algorithm has to discover and model hidden relationships between the feature space and the outcome space and create links between the two. Doing so requires overcoming barriers such as feature noise (randomness of features due to unexplained mechanisms).
In this article we argue that “Emergence” is also a barrier for predictive inference. Emergence is a phenomenon through which a completely new entity arises (emerges) from interactions among elementary entities such that the emerged entity exhibits properties the elementary entities do not exhibit. We present the idea that success of machine learning, and predictive inference in general, can be adversely affected by the phenomena of emergence. We argue that this phenomena might be partially responsible for unsuccessful use of current ML algorithms in some situations such as stock markets.
Emergence
Emergence is a fundamental concept in theories of complex systems [1] [2] . For example, consider the phenomenon of life as studied in biology. It is an emergent property of chemistry: life emerges from interactions between complex proteins. But life is more than just a collection of complex proteins. This is generally known as “the whole is more than sum of its parts.” Another example is psychological phenomena, which emerge from the neurobiological phenomena of living things. An emergent property of a system, is not a property of any of the primitive (elementary) parts of that system, but is still a feature of the system as a whole.
My favorite example is ant colony: ants independently (autonomously) react to stimuli by producing chemical scents known as pheromones, which in turn leaves a trail for other ants. They don’t receive orders from the queen or any other ant, which means that the colony acts as a decentralized system. Ant colonies exhibit complex behaviors and a level of intelligence (known as swarm intelligence) far beyond any individual ant’s intelligence. For example, colonies routinely find optimal paths to food, create living bridges and boats by interlocking their bodies together and they find the maximum distance from all colony entrances to dispose of dead bodies.
Strong and Weak Emergence
In complex systems theory, philosophers describe two kinds of emergence phenomena: the newer notion of “weak emergence” and the older notion of “strong emergence” [2] [3] . Weak emergence occurs when the emergent properties can be understood by observing or simulating the system, and not by any process of a priori analysis. On the other hand, in strong emergence the emergent qualities are irreducible to the system’s part (the system is other than the sum of its parts). Unlike weak emergence, a strong emergent phenomenon cannot be simulated by a computer (at least by today’s systems). An example of such emergence is water, properties of which are unpredictable even after a study of the properties of its integral atoms: hydrogen and oxygen.
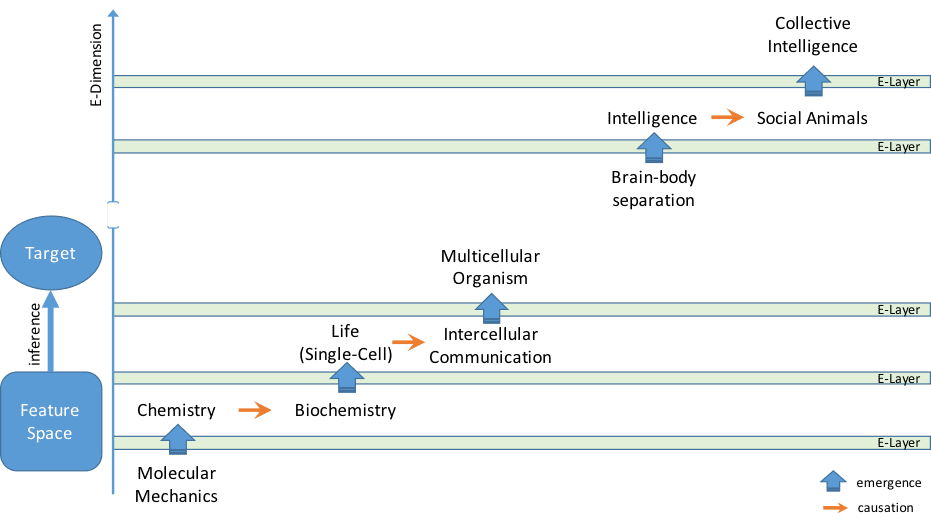
Figure 1. Hypothetical example of the E-Dimension concept. Emergence phenomena can be considered as a barrier for making predictive inferences. The further away the target is from features along this dimension, the less information the features provide about the target. The figure shows an example of predicting organism level properties (target) using molecular and physicochemical properties (feature space).
The E-Dimension
We propose that, in predictive inference context, emergence can be thought of as a dimension. As we go further along this dimension, emergent properties begin to appear. A hypothetical example is shown in Figure 1. As discussed above, emergence creates barriers for making predictive inferences, as a result one should be mindful of the emergence phenomena when making predictive inference.
The barrier is stronger when it consists of several levels (layers) of emergent phenomena (we call them E-layers). To better explain this notion, let P be a physical state caused by another physical state Q. Let E be an emergent property that supervene on physical state P (e.g. primitive intelligence supervenes on interactions among neurons caused by biochemical properties and signaling pathways). Let E* be another emergent property supervene on base property P* where P* is caused by E (e.g. social behavior which supervenes on emotional intelligence/self-awareness caused by primitive intelligence). To make predictive inference from Q to P, there’s no emergence barrier, thus no E-layer needs to be crossed. However, inferencing from Q to E (e.g. predicting properties of intelligence using biochemical features), means crossing at least 1 E-layer, and from Q to E* (e.g. predicting properties of social behavior using biochemical features), at least 2 E-layers.
The larger the number of E-layer barriers, the less amount of information a feature can provide on the outcome due to the emergence phenomena.
Some examples in ML
Stock prediction: The stock market (or any other similar market) is a remarkable example of emergence. It, as a whole, has no leader and no centralized command and control center, yet it precisely regulates the relative security prices of companies globally. Predicting stock values means using publicly available data and historic stock prices to determine whether or not the value will increase. Feature space includes historic stock values, related company features, news articles, etc. Outcome is the future stock values. Emergence layer(s) involve collective buying/selling behavior, emerged from individuals’ decisions. There is not much feature noise in collecting stock prices, since exact values are publicly available [13].
Character/Image recognition: In character recognition problem, there is not much emergence phenomena involved. Relative locations of pixels on an image directly provide information about the image. This is why for example automatic license plate readers work accurately almost always. Feature space may be handwritten character images. Outcome is the character. Feature noise exists due to variations between handwritings and/or images [4].
Weather prediction: Contrary to other examples in this article, modern weather prediction is not done merely by using ML methods. Instead, it’s done by sampling the state of the weather at a given time and using the equations of fluid dynamics and thermodynamics to estimate the state of the fluid at some time in the future. By leveraging the knowledge of physical mechanisms that generate the outcome, this method has been relatively successful overcoming the weak emergence barrier. I believe the ML community can potentially learn valuable lessons from weather prediction methods [6].
Table 1. Effect of emergence on example ML problems

Conclusion
In this article we discussed possible effects of emergence phenomena on predictive inference and in turn on Machine Learning methods. Emergence phenomena occur in complex systems where elementary parts interact with each other and give rise to totally new properties at a different level. We argue that emergence can be thought of as a serious barrier for making predictive inference. The concept of E-Dimension in predictive inference is introduced. Being mindful of emergence phenomena in designing predictive inference engines provides valuable insight into engineering better features and more effectively cross emergence barriers.
Further research is needed to better model the effects of emergence phenomena (such as the work done in [14] and [15] ). A new class of ML algorithms is needed that can model emergence phenomena more effectively and make more accurate predictions in presence of emergence.
References
[1] Anderson, P. W. (1994). More is different: Broken Symmetry and the Nature of the Hierarchical Structure of Science. Science, 177(4047), 393-396.
[2] Bedau, M. A. (1997). Weak emergence. Noûs, 31(s11), 375-399.
[3] Chalmers, D. J. (2006). Strong and weak emergence. In P. Clayton and P. Davies, eds. The Re-emergence of Emergence. Oxford University Press, 244-256.
[4] Du, S., Ibrahim, M., Shehata, M., & Badawy, W. (2013). Automatic license plate recognition (ALPR): A state-of-the-art review. IEEE Transactions on circuits and systems for video technology, 23(2), 311-325.
[5] Xiong, W., Droppo, J., Huang, X., Seide, F., Seltzer, M., Stolcke, A., … & Zweig, G. (2016). Achieving human parity in conversational speech recognition. arXiv preprint arXiv:1610.05256.
[6] Bauer, P., Thorpe, A., & Brunet, G. (2015). The quiet revolution of numerical weather prediction. Nature, 525(7567), 47-55.
[7] He, C., Parra, D., & Verbert, K. (2016). Interactive recommender systems: A survey of the state of the art and future research challenges and opportunities. Expert Systems with Applications, 56, 9-27.
[8] Cacheda, F., Barbieri, N., & Blanco, R. (2017, February). Click Through Rate Prediction for Local Search Results. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining (pp. 171-180). ACM.
[9] Ghosh, T., Sarkar, D., Sharma, T., Desai, A., & Bali, R. (2016, December). Real Time Failure Prediction of Load Balancers and Firewalls. In Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), 2016 IEEE International Conference on (pp. 822-827). IEEE.
[10] Golmohammadi, D., & Radnia, N. (2016). Prediction modeling and pattern recognition for patient readmission. International Journal of Production Economics, 171, 151-161.
[11] Hughes, L. D., Palmer, D. S., Nigsch, F., & Mitchell, J. B. (2008). Why are some properties more difficult to predict than others? A study of QSPR models of solubility, melting point, and Log P. Journal of chemical information and modeling, 48(1), 220-232.
[12] Tetko, I. V., Sushko, Y., Novotarskyi, S., Patiny, L., Kondratov, I., Petrenko, A. E., … & Asiri, A. M. (2014). How accurately can we predict the melting points of drug-like compounds? Journal of chemical information and modeling, 54(12), 3320-3329.
[13] Agrawal, J. G., Chourasia, V. S., & Mittra, A. K. (2013). State-of-the-art in stock prediction techniques. International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, 2(4), 1360-1366.
[14] Teo, Y. M. (2016). Modelling and Formalizing Emergence. In Intelligent Systems, Modelling and Simulation (ISMS), 2016 7th International Conference on (pp. 3-4). IEEE.
[15] Heylighen, F. (1991). Modelling emergence. World Futures: Journal of General Evolution, 32(2-3), 151-166.
