
- New study successfully tackles the problem of dimensionality reduction in embedded systems.
- The reduced model can be implemented without loss of accuracy.
- Combining POD with FNN resulted in decreased training time.
Artificial Neural Networks (ANNs) are used in a wide variety of applications from forecasting to speech recognition. Memory and space constraints sometimes call for a reduced network. However, this can result in loss of accuracy, because accuracy of an ANN is related to the number of inputs, layers, and neurons. A recent paper called A Dimensionality Reduction Approach for Convolutional Neural Networks [1], published 19 October, suggests an improved method for producing a reduced, yet robust, version of the original network. Although similar studies have tackled this problem before, this study was unique in that it produced a generic, highly adaptable framework that performs better than its predecessors. The study culminated in an ANN that can be implemented on an embedded system without loss of accuracy.
The Reduction Problem in Embedded Systems
Embedded systems are microprocessor-based hardware systems with software that performs a dedicated function [2]. These systems often have limited hardware, with memory and space constraints. Implementing an ANN in an embedded system is problematic because complex tasks require very deep architectures with many hidden layers. Arbitrary reduction isnt possible because, after many iterations of training and testing on multiple models, one model gives the best results. Therefore, reducing the model usually means that the “best” model is no longer viable.
The authors tackled this problem by exploiting Active Subspace (AS) property and Proper Orthogonal Decomposition (POD), two tools widely used to reduce the dimensionality of intermediate convolutive features. Although AS and POD were the focus of the study, the result was a generic artificial neural network (ANN) which can be tailored to suit by substituting AS and POD with other dimensionality reduction methods.
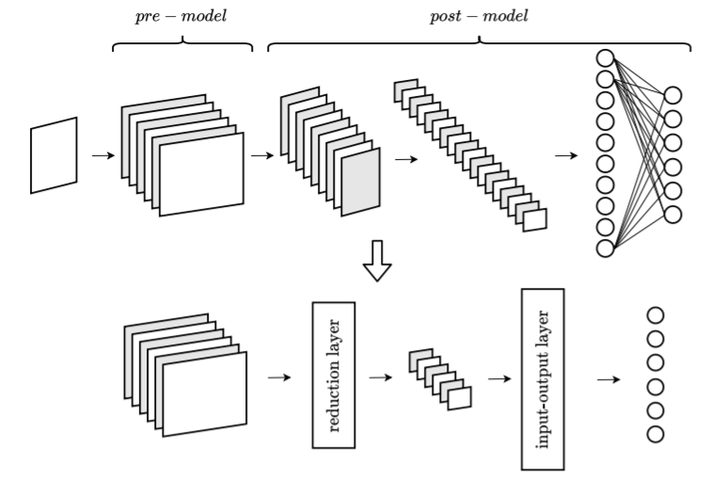
The authors reduced the model, shown in the above image, in a series of steps:
- Network splitting: The original network was split into two parts: pre-model and post-model. An index specified the cut-off layer, which defined how many layers of the original network were kept.
- Dimensionality reduction was performed with AS and POD.
- Input-output mapping: Output coming from the reduction layer was classified with Polynomial Chaos Expansion, which is a way of representing a random variable as a function of another random variable and representing that function as a polynomial expansion [3]. A Feedforward Neural Network (FNN) was also used, where information only moves forward (i.e., it isnt cyclical).
After the reduced network was constructed, it was trained using knowledge distillation, where a small student model is trained under the guide of a larger, pre-trained teacher model. The network was tested on two different object recognition datasets using a Convoluted Neural Network (CNN). The result was a reduced model (in terms of layers and parameters) that can successfully be employed on an embedded system, without loss of accuracy. An added bonus was that the authors found the combination of POD and FNN resulted in a decreased training timean improvement on previous research.
The technique does have one drawbackthe model can only be reduced with an already trained network. Despite saving memory and space, the learning procedure became a bottleneck for many problems. However, the authors conclude that it is possible to extend the framework to reduce dimensions during the training.
References
Image: (Neural Network): Adobe Creative Cloud
[1] A Dimensionality Reduction Approach for Convolutional Neural Networks
[2] What is an Embedded System?
[3]Polynomial Chaos: A Tutorial and Critique from a Statisticians Per…
