Swarm Optimization: Goodbye Gradients

Fish schools, bird flocks, and bee swarms. These combinations of real-time biological systems can blend knowledge, exploration, and exploitation to unify intelligence and solve problems more efficiently. There’s no centralized control. These simple agents interact locally, within their environment, and new behaviors emerge from the group as a whole. In the world of evolutionary alogirthms one such inspired method is particle swarm optimization (PSO). It is a swarm intelligence based computational technique that can be used to find an approximate solution to a problem by iteratively trying to search candidate solutions (called particles) with regard to a given measure of quality around a global optimum. The movements of the particles are guided by their own best known position in the search-space as well as the entire swarm’s best known position. PSO makes few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. As a global optimization method PSO does not use the gradient of the problem being optimized, which means PSO does not require that the optimization problem be differentiable as is required by classic optimization methods such as gradient descent. This makes it a widely popular optimizer for many nonconvex or nondifferentiable problems. A brief review of applications that may be of interest to data scientists include:

Hyperparameter optimization for deep learning models [1].
Training different neural networks [2].
Learning to play video games [3].
Natural language processing tasks [4].
Data clustering [5].
Feature selection in classification [6].

In 1995, Dr. Eberhart and Dr. Kennedy developed PSO as a population based stochastic optimization strategy inspired by the social behavior of a ﬂock of birds. When using PSO, a possible solution to the numeric optimization problem under investigation is represented by the position of a particle. Each particle has a current velocity, which represents a magnitude and direction toward a new, presumably better, solution. A particle also has a measure of the quality of its current position, the particle’s best known position (a previous position with the best known quality), and the quality of the global best known position of the swarm. In other words, in a PSO system, particles ﬂy around in a multidimensional search space. During ﬂight, each particle adjusts its position according to its own experience, and according to the experience of a neighboring particle, making use of the best position encountered by itself and its neighbor.

The PSO algorithm keeps track of three global variables: target value, global best (gBest) value indicating which particle’s data in the population is currently closest to the target, and stopping value indicating when the algorithm should stop if the target isn’t found. The particle associated with the best solution (ﬁtness value) is the leader and each particle keeps track of its coordinates in the problem space. Basically each particle consists of: data representing a possible solution, a velocity value indicating how much the data can be changed, and a personal best (pBest) ﬁtness value indicating the closest the particle’s data has ever come to the target since the algorithm started. The particles data could be anything. For example, in a flock of birds flying over a food source, the data would be the X, Y, Z coordinates of each bird. The individual coordinates of each bird would try to move closer to the coordinates of the bird (gBest) which is closer to the food’s coordinates. The gBest value only changes when any particle’s pBest value comes closer to the target than gBest. At each iteration of the algorithm, gBest gradually moves closer and closer to the target until one of the particles reaches the target. If the data is a pattern or sequence, then individual pieces of the data would be manipulated until the pattern matches the target pattern.

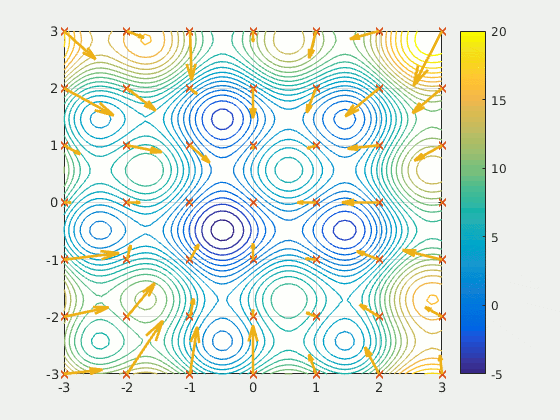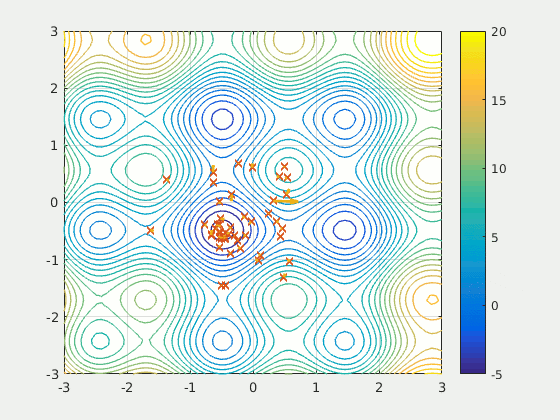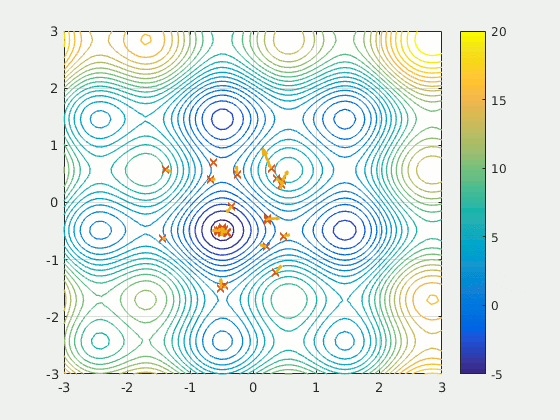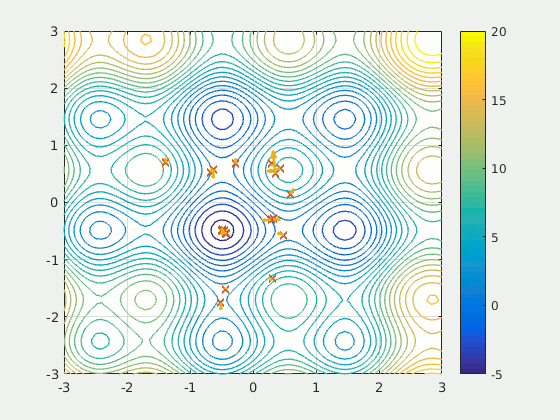Figure: A particle swarm searching for the global minimum of a function (Source: Wikipedia).

The velocity value is calculated according to how far an individual’s data is from the target. The further it is, the larger the velocity value. In the bird example, the individuals furthest from the food would make an effort to keep up with the others by flying faster toward the gBest bird. If the data is a pattern or sequence, the velocity would describe how different the pattern is from the target, and thus, how much it needs to be changed to match the target. The swarm of particles initialized with a population of random candidate solutions move through the D-dimension problem space to search the new solutions. The ﬁtness, f, can be calculated as the certain qualities measure. Each particle has a position represented by a position-vector and a velocity. The update of the particles velocity from the previous velocity to the new one is determined by the following equation:

From this a particle decides where to move next, considering its own experience, which is the memory of its best past position, and the experience of its most successful particle in the swarm. The new position is then determined by the sum of the previous position and the new velocity. In a more mathematical notation the previous two equations could be defined as:

The first equation updates a particle’s velocity which is a vector value with multiple components. The term $\overrightarrow{v}_{i}(t+1)$ means the new velocity at time $t+1$ . The new velocity depends on three terms. The first term is $latex \overrightarrow{v}_{i}(t) $ which is the current velocity at time $t$ . The second part is $c_{1} \phi_{1} (\overrightarrow{p}_{i}(t) - \overrightarrow{x}_{i}(t))$ . The $c_{1}$ term is a positive constant called as coefficient of the self-recognition component. The $\phi_{1}$ and $\phi_{2}$ factors are uniformly distributed random numbers in [0,1]. The $\overrightarrow{p}_{i}(t)$ vector value is the particle’s best position found so far. The $\overrightarrow{x}_{i}(t)$ vector value is the particle’s current position. The third term in the velocity update equation is $c_{2} \phi_{2} (\overrightarrow{p}_{g}(t) - \overrightarrow{x}_{i}(t))$ . The $c_{2}$ factor is a constant called the coefficient of the social component. The $\overrightarrow{p}_{g}(t)$ vector value is the best known position found by any particle in the swarm so far. Once the new velocity, $\overrightarrow{v}_{i}(t+1)$ , has been determined, it’s used to compute the new particle position $\overrightarrow{x}_{i}(t+1)$ . The term $\overrightarrow{v}_{i}$ is limited to the range $\pm \overrightarrow{v}_{max}$ . If the velocity exceeds this limit, it is set to it.

PSO does not require a large number of parameters to be initialized. But the choice of PSO parameters can have a large impact on optimization performance and has been the subject of much research. The number of particles is a very important factor to be considered. For most of the practical applications an example good choice of the number of particles is typically in the range [20,40]. Usually 10 particles is a large number which is sufficient enough to get best results. In case of difficult problems the choice can be increased to 100 or 200 particles. The parameters $c_{1}$ and $c_{2}$ , coefficient of self-recognition and social components, are critical for the convergence of the PSO algorithm. Fine-tuning of these learning vectors aids in faster convergence and alleviation of local minima. Usually the choice for these parameters is 2.

Below is the full PSO algorithm shown as a flow chart:

References:

[1] Lorenzo, Pablo Ribalta, et al. “Particle swarm optimization for hyper-parameter selection in deep neural networks.” Proceedings of the Genetic and Evolutionary Computation Conference. ACM, 2017.

[2] Gudise, Venu G., and Ganesh K. Venayagamoorthy. “Comparison of particle swarm optimization and backpropagation as training algorithms for neural networks.” Swarm Intelligence Symposium, 2003. SIS’03. Proceedings of the 2003 IEEE. IEEE, 2003.

[3] Singh, Garima, and Kusum Deep. “Role of Particle Swarm Optimization in Computer Games.” Proceedings of Fourth International Conference on Soft Computing for Problem Solving. Springer, New Delhi, 2015.

[4] Tambouratzis, George. “Applying PSO to natural language processing tasks: Optimizing the identification of syntactic phrases.” Evolutionary Computation (CEC), 2016 IEEE Congress on. IEEE, 2016.

[5] Chuang, Li-Yeh, Chih-Jen Hsiao, and Cheng-Hong Yang. “Chaotic particle swarm optimization for data clustering.” Expert systems with Applications 38.12 (2011): 14555-14563.

[6] Xue, Bing, Mengjie Zhang, and Will N. Browne. “Particle swarm optimization for feature selection in classification: A multi-objective approach.” IEEE transactions on cybernetics 43.6 (2013): 1656-1671.

Leave a Reply Cancel reply