The following problems appeared in the exercises in the Coursera course Image Processing (by Northwestern University). The following descriptions of the problems are taken directly from the exercises’ descriptions.
1. Analysis of an Image quality after applying an nxn Low Pass Filter (LPF) for different n
The next figure shows the problem statement. Although it was originally implemented in MATLAB, in this article a python implementation is going to be described.

The following figure shows how the images get more and more blurred after the application of the nxn LPF as n increases.

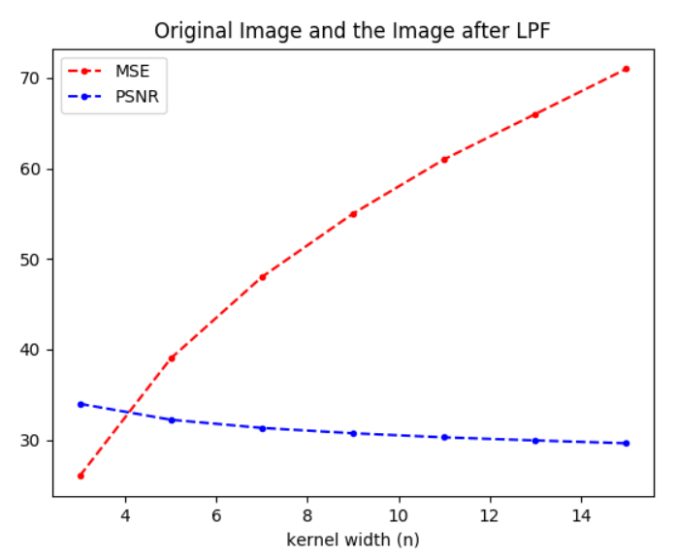
The following figure shows how the quality of the transformed image decreases when compared to the original image, when an nxn LPF is applied and how the quality (measured in terms of PSNR) degrades as n (LPF kernel width) increases.
2. Changing Resolution of an Image with Down/Up-Sampling
The following figure describes the problem:

The following steps are needed to be followed:
- Smooth the original image with a 3×3 LPF (box1) kernel.
- Downsample (choose pixels corresponding to every odd rows and columns)
- Upsample the image (double the width and height)
- Use the kernel and use it for convolution with the upsampled image to obtain the final image.
Although in the original implementation MATLAB was used, but the following results come from a python implementation.

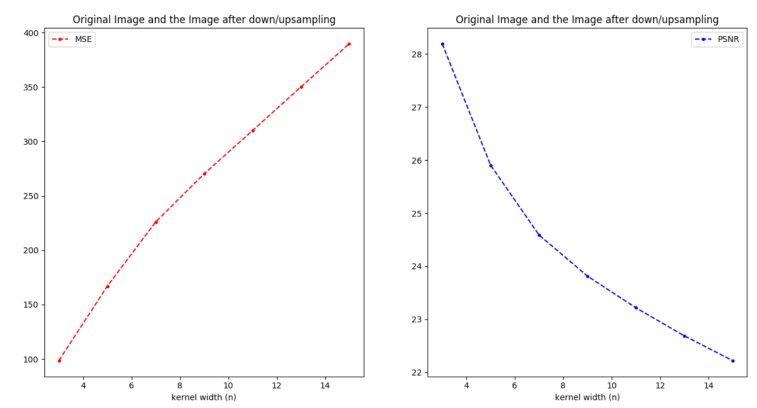
As we go on increasing the kernel size, the quality fo the final image obtained by down/up sampling the original image decreases as n increases, as shown in the following figure.
3. Motion Estimation in Videos using Block matching between consecutive video frames
The following figure describes the problem:

For example we are provided with the input image with known location of an object (face marked with a rectangle) as shown below.

Now we are provided with another image which is the next frame extracted from the same video but with the face unmarked) as shown below. The problem is that we have to locate the face in this next frame and mark it using simple block matching technique (and thereby estimate the motion).

As shown below, using just the simple block matching, we can mark the face in the very next frame.

Now let’s play with the following two videos. The first one is the video of some students working on a university corridor, as shown below (obtained from youtube), extract some consecutive frames, mark a face in one image and use that image to mark all thew faces om the remaining frames that are consecutive to each other, thereby mark the entire video and estimate the motion using the simple block matching technique only.

The following figure shows the frame with the face marked, now we shall use this image and block matching technique to estimate the motion of the student in the video, by marking his face in all the consecutive frames and reconstructing the video, as shown below..




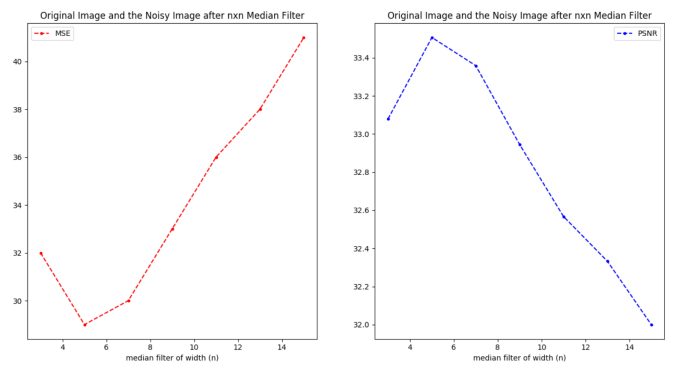
4. Using Median Fiter to remove salt and paper noise from an image
The following figure describes the problem:
The following figure shows the original image, the noisy image and images obtained after applying the median filter of different sizes (nxn, for different values of n):

As can be seen from the following figure, the optimal median filter size is 5×5, which generates the highest quality output, when compared to the original image.
Using Inverse Filter to Restore noisy images with Motion Blurs
The following figure shows the description of the problem:
The following figure shows the theory behind the inverse filters in the (frequency) spectral domain.

- Generate restoration filter in the frequency domain (with Fast Fourier Transform) from frequency response of motion blur and using the threshold T.
- Get the spectrum of blurred and noisy-corrupted image (the input to restoration).
- Compute spectrum of restored image by convolving the restoration filter with the blurred noisy image in the frequency domain.
- Genrate the restored image from its spectrum (with inverse Fourier Transform).
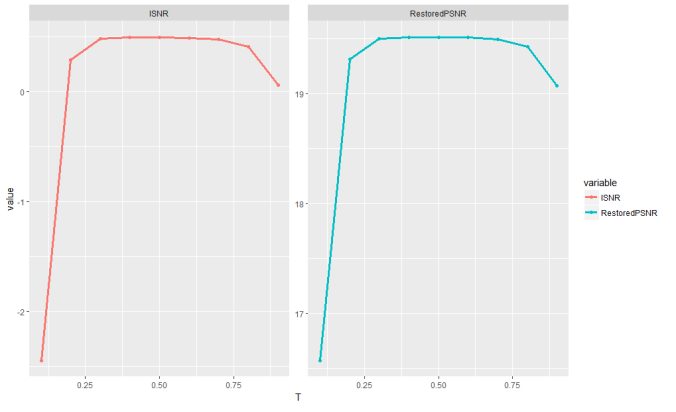
The following figures show the inverse filter is applied with different threshold value T (starting from 0.1 to 0.9 in that order) to restore the noisy / blurred image.









The following figure shows how the Restored PSNR and the ISNR varies with different values if the threshold T.