- Statistics comes in two flavors: Bayesian and Frequentist,
- Both methods have their opponents and proponents,
- You should learn both to enhance your modeling.
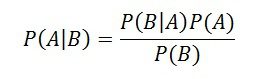In statistical inference, you have the choice between Bayesian and frequentist [no term] (classical) approaches. At first glance, Bayesian methods are faster, cleaner and more user-friendly. It’s often thought to be a more intuitive approach to analysis, more closely mimicking how our brains tackle problems–making it more user friendly. So why aren’t we all using Bayesian methods?
At first glance, Bayesian methods are a step up from the frequentist approach, with proponents touting its many advantages, including:
- Faster learning: With a frequentist approach, you base your opinions on facts you glean from data. With Bayesian analysis, you start with an initial belief, then gather evidence–adapting your initial beliefs to the evidence. Building on those previous results leads to faster learning [1].
- Easier to interpret: Bayesian methods have more flexible models. This flexibility can create models for complex statistical problems where frequentist methods fail. In addition, the results from Bayesian analysis are often easier to interpret than their frequentist counterparts [2].
- Better, more user-friendly results: According to Matthew Kay and colleagues at the University of Washington’s school of Computer Science & Engineering Bayesian analysis [3] frees researchers from the “shackles shackles of meaningless p-values [no term] ” in small sample studies, Instead, you concentrate on probable effect sizes [no term]. This allows many more smaller studies to be included in the conversation instead of being buried under a haze of uncertain significance. The researchers claim that Bayesian statistics are more user-centered.
Bayesian analysis is behind a swath of artificial-intelligence research, including Google’s self-driving cars. According to Sharon Bertsch McGrayne [4], author of A popular history of Bayes’ theorem, Bayesian analysis can “sort spam from e-mail, assess medical and homeland security risks and decode DNA, among other things.”
Given all the above, it seems surprising that we don’t throw out those old frequentist methods in favor of this newer, user friendly set of tools that’s on the forefront of AI. So why aren’t we adopting these great tools on masse? Perhaps because the statistical branch is as problematic as its frequentist predecessor.
The “Pseudoscience “of Bayesian Statistics
Andrew Gelman, professor of statistics and political science at Columbia University, states that a major problem with Bayesian methods is in how those methods have evolved over time. “In the old days, Bayesian methods at least had the virtue of being mathematically clean,” says Gelman. “Nowadays, they all seem to be computed using Markov chain Monte Carlo, which means that not only can you not realistically evaluate the statistical properties of the method, you can’t even be sure it’s converged [no term], just adding one more item to the list of unverifiable (and unverified) assumptions” [5]
So, as useful as Bayesian statistics might appear to be, be aware that your carefully implemented algorithms might be brushed away as pseudoscience–especially if you’re using MCMC.
But couldn’t the pseudoscience label also be applied to frequentist statistics? After all, the “usual” statistics” is famous for it’s capability to easily warp the truth. At the core of the frequentist approach is the p-value , notorious for it’s flexibility–and that’s not in a good sense. For example, P-Hacking–where you add covariates, remove outliers or perform other statistical magic to turn your large p-value into a small one–is just one way how p-values can be easily manipulated to make results fit an agenda.
Why You Should Learn Bayesian Statistics Anyway
If Bayesian statistics are just as problematic as frequentist methods, the solution to all the pseudoscience is to learn them both. Ken Rice, professor of biostatistics for the University of Washington, says it best:
“Using a spade for some jobs and shovel for others does not require you to sign up to a lifetime of using only Spadian or Shovelist philosophy, or to believing that only spades or only shovels represent the One True Path to garden neatness.” [6]
You shouldn’t vote in an election without researching all of the candidates and making an informed decision about which one is “best”. By the same token, you are hobbling your ability to effectively analyze data if you constrain yourself to a single set of techniques, especially when the utility of both methods are under debate. By learning both Bayesian and Frequentist methods, you give yourself the ability to choose the best candidate for the task at hand.
References
[1] TEACHING BAYESIAN STATISTICS TO UNDERGRADUATES: WHO, WHAT, WHERE, W…
[2] Introduction to Bayesian Statistics in Life Sciences- FNR 6560
[3] Researcher-Centered Design of Statistics: Why Bayesian Statistics B…
[4] Why Bayes Rules: The History of a Formula That Drives Modern Life
