This is an interesting data science conjecture, inspired by the well known six degrees of separation problem, stating that there is a link involving no more than 6 connections between any two people on Earth, say between you and anyone living (say) in North Korea.
Here the link is between any two univariate data sets of the same size, say Data A and Data B. The claim is that there is a chain involving no more than 6 intermediary data sets, each highly correlated to the previous one (with a correlation above 0.8), between Data A and Data B. The concept is illustrated in the example below, where only 4 intermediary data sets (labeled Degree 1, Degree 2, Degree 3, and Degree 4) are actually needed. The numbers highlighted in red show how this chain of data sets is built.
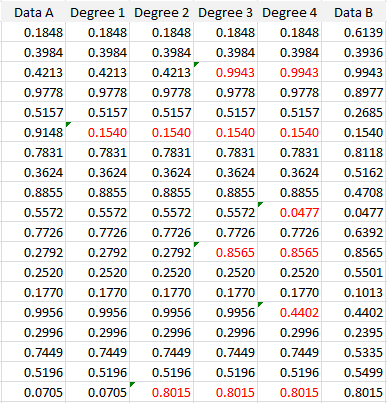
We have the following correlations:
- Between Data A and Data B: -0.0044
- Between Degree 1 and Data A: 0.8232
- Between Degree 2 and Degree 1: 0.8293
- Between Degree 3 and Degree 2: 0.8056
- Between Degree 4 and Degree 3: 0.8460
- Between Data B and Degree 4: 0.8069
Note that the data sets A and B were randomly generated, using the RAND() function in Excel. The full correlation table is as follows:
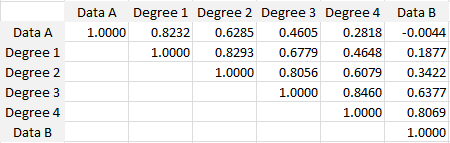
Cross-correlations between the 6 data sets
Conclusions
This is just a conjecture, and maybe the number of intermediary data sets or the 0.8 correlation must be fine-tuned and could depend on the size of the data set. But it makes for an interesting theoretical data science research project, for people with too much free time on their hands.
In some way, one could say that anything is related to everything, by a short path. Or that anything is caused by everything. This has of course been exploited in many news outlets to convey a political message, or to cause you to click on some random, worthless article, by using subject lines that seem implausible to attract your attention.
About the Author
Vincent Granville is a machine learning scientist, author and publisher. He was the co-founder of Data Science Central (acquired by TechTarget) and most recently, founder of Machine Learning Recipes.
