In a previous post, I have provided a discussion of model stacking, a popular approach in data science competitions for boosting predictive performance. Since then, the post has attracted some attention, so I have decided to put together a Python package which provides a simple API to stack models with minimal effort.
In this post, I will present the Pancake package, which is designed to simplify the stacking process and help the user experiment with stacking efficiently. For readers who are new to model stacking, I recommend reading the previous post first. For readers who would like to learn the implementation details, I recommend going over the documentation in the repository.
There are several packages out there which provide user friendly APIs for stacking (in Python and R). The Pancake package differs mostly in the way stacking is implemented. Additionally, I have tried to document the fine details as clearly as possible to provide the user with the inner workings of the stacking process.
Recap
Stacking works by training/fitting several models on a given number of splits of data. The splitting is a reminiscent of k-folds cross-validation, and each model is fit on k-1 folds of data and predictions on the kth fold are stacked to obtain out-of-sample (OOS) predictions. These out-of-sample predictions are then used as the new data for a stacker model, which is then trained over the k-folds and returns final predictions. In other words, the stacker model uses predictions from stacked models as features.
The figure below shows one step of stacking that uses 5 folds. The first fold is kept as hold-out (HO) data, while the rest of the folds are used to construct the OOS predictions for a given number of models.
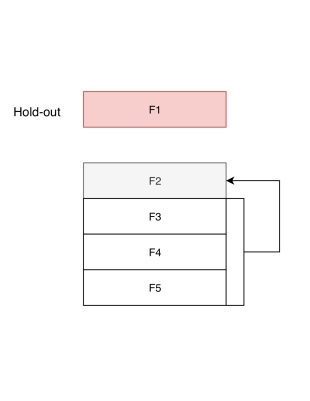 An example of data splitting for model stacking. All models are fit on folds 3,4,5 and the predictions on fold 2 are stored as a part of OOS predictions.
An example of data splitting for model stacking. All models are fit on folds 3,4,5 and the predictions on fold 2 are stored as a part of OOS predictions.There are five possible choices of HO data and stacking uses all of them to construct 5 pairs of (OOS,HO) splits. These five pairs are then used by the stacker model for training, i.e. a stacker is fit on OOS and predictions are obtained on the HO. A hyper-parameter grid for the stacker model is used to pick the best hyper-parameter(s) in this step, which is equivalent to 5-folds cross-validation.
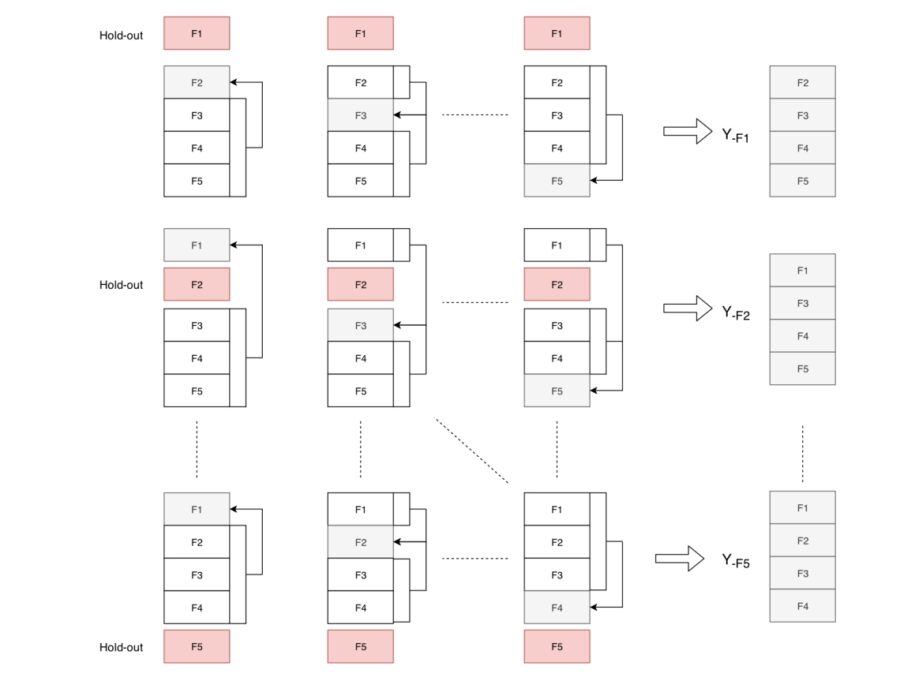
All possible HO/OOS data in case of 5-folds splitting.
The figure above illustrates all HO and OOS data obtained from fitting a single model across all 5 folds, which are then used by the stacker model(s).
One goes through all the trouble of stacking multiple models across folds in order to boost the performance of initial models by combining them. The combination is performed by out-of-sample predictions, which provides good generalizability and reduces chances of over-fitting. Further details on why stacking works can be found in the previous post.
Implementation of Stacking
The package is designed to allow the user add multiple input (in-layer) and stacker (out-layer) models and train the stacked model easily. A typical layout of the of the pipeline is illustrated in the figure below:
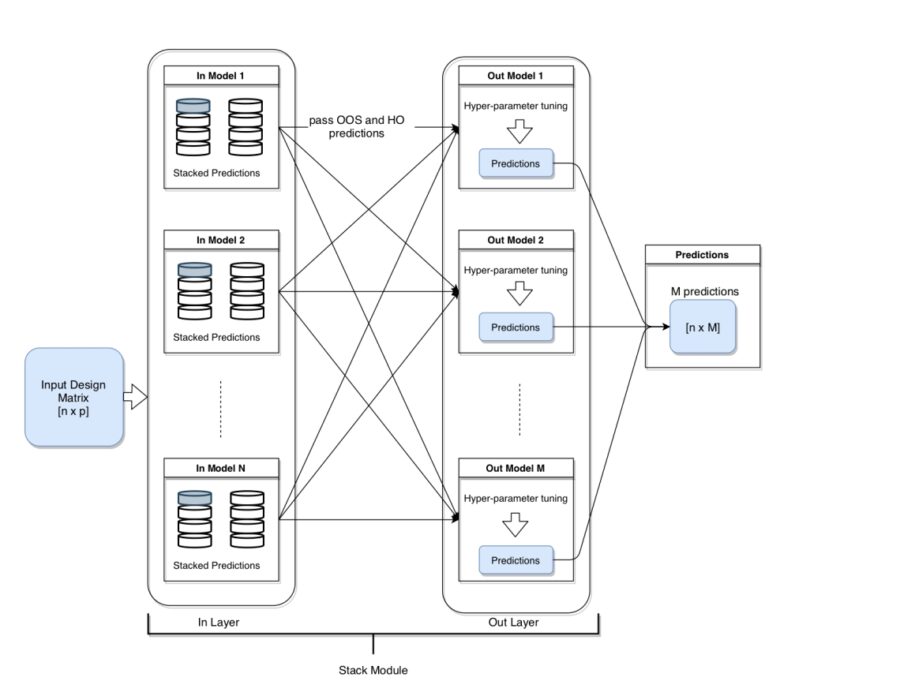 Architecture of model stacking across N in-layer and M out-layer models.
Architecture of model stacking across N in-layer and M out-layer models.
The “stacker module” is composed of two layers: (i) in-layer taking the models to be stacked, (ii) out-layer containing the stacker models. Most common applications of stacking involves a single stacker model, but I have decided to include the capability to have multiple stacker models in a out-layer for reasons that will be clear below.
As input, the module takes in the data, the number of folds to be used in stacking, in-layer and out-layer models. The in-layer then trains/fits these input models over the folds and transfers the out-of-sample (OOS) and hold-out (HO) predictions to the out-layer. Each out-layer model is trained and the predictions are collected in an output matrix. Each column in the output matrix are the stacked predictions from each out-layer model. At this point the user can either (i) choose one column as final predictions, (ii) average column-wise for final predictions, (iii) or even treat the output matrix as the new data and use it in another stacking module!
Usage
The basic usage of the package is explained in the repository. The user simply provides the data, the splits as a cross-validation generator, the desired models (scikit-learn objects) and hyper-parameter grids to the stacker. The stacker implements simple methods to add models, and predict/train on training and test data.
Application in Boston Housing Data
I have included two Python notebooks in the repository, which use the Boston Housing dataset (available in scikit-learn) to illustrate the use of the package. Below are the results for stacking two linear (Ridge Regression and Lasso) and two non-linear (Random Forest and Support Vector Regression) models. In both cases, the stacked model does slightly better.
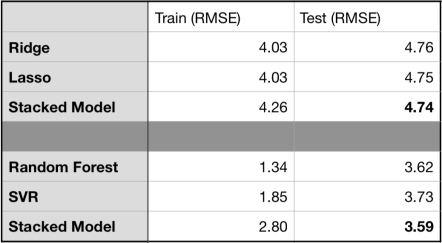 Stacking two linear and two non-linear models for the Boston Housing data. The stacked models in both cases perform slightly better in the test set.
Stacking two linear and two non-linear models for the Boston Housing data. The stacked models in both cases perform slightly better in the test set.Stacking usually results in better performance, when the input models are quite different. This can actually be seen in the results above, where stacking two similar linear models (Lasso and Ridge) does not do as good as two different models (Random Forest and SVR). One way to check how different the initial models are is by computing the correlation between their prediction vectors.
Final Words
The aim of the Pancake package is to provide the user a simple API to experiment with stacking models with minimal effort. There will be additions and improvements to the package (like parallelization) as I find time to work on it.
A word of caution is that stacked models are not always guaranteed to lead to better results compared to single models. Usually, the improvements in the predictive performances are minuscule. In some cases, if the stacked models are not chosen properly, the overall performance could even get worse. These are topics that I will touch on (hopefully) in a later post.
The original blog post was posted in the author’s site.
