There are many ways to deal with time-data. Sometimes one can use it as time-series to take possible trends into account. Sometimes this is not possible because time can not be arranged in a sequence. For example, if there are just weekdays (1 to 7) in a dataset over several month. In this case one could use one-hot-encoding. However, considering minutes or seconds of a day one-hot-encoding might lead to high complexity. Another approach is to make time cyclical. This approach leads to a lower dimensionality and (maybe) a better predictive power.
But what does cyclical time mean?
Cyclical time is a concept that assumes that time is a circle. Sunday 12:00 midnight is the same as Monday 0:00 am. The end of the last second of the previous year is the same as the start of the first second of the next year etc. Whether this approach is appropriate one can prove by cross validation or the correlation with the target feature.
How to make data cyclical?
In many blog-posts it is recommended to use a sine function. For example, for seven weekdays like (blue):
value = sin(2π*time/7)
or from zero to zero over one week (green):
value = sin(2π*time/14)
or two cycles over the week (red):
value = sin(2π*time/3.5)
Let’s take a look at the function “value”:
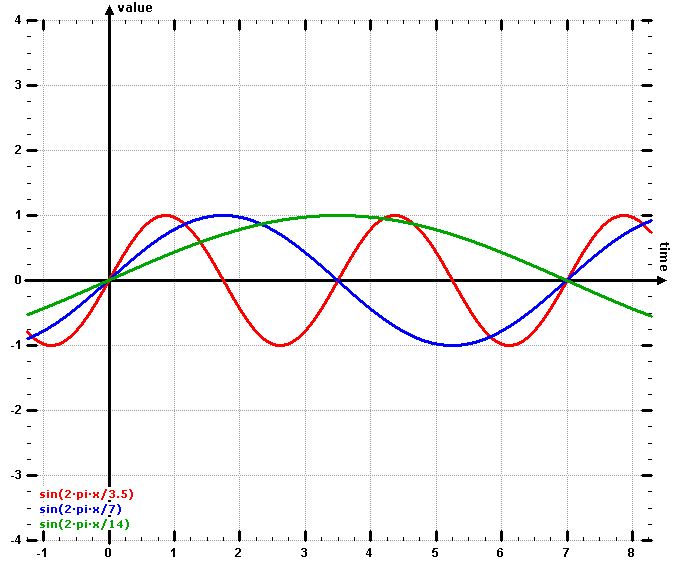
figure created by wzgrapher
But how many cycles are there over a specific time period?
It depends on the case – and the data. If there is a solid theory why there must be 2, 4, or 8 cycles; perfect. Nevertheless, one must check how many cycles are appropriate.
Furthermore, it is not clear when the cycle starts. In case of a week on Monday, Sunday, or Saturday…?
A good idea is to shift the start (respectively the end) of the period (week). For example, making Saturday to the first day of the week. (Don’t forget to validate which shift is the best)
Now, let me introduce an alternative approach which sometimes leads to better results than a sine function.
Starting with a three-dimensional function:
cycle = time^2+value^2
solve to “value”:
value = (cycle – time^2)^0.5
Let’s look at “value” by setting cycle equal to one = red, two = blue, three = green:
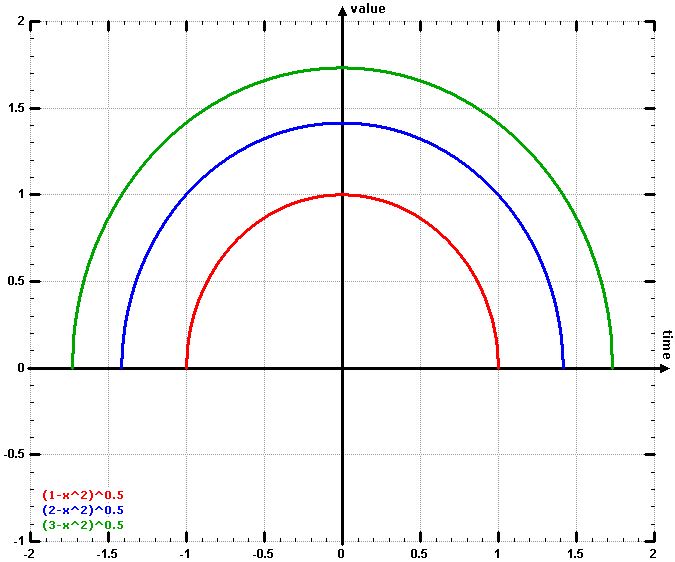
figure created by wzgrapher
This function has two important features:
1) The diameter is determined by “cycle”
2) It is a circle that the radius is diameter / 2
So, to adjust the function to seven weekdays one must find a diameter of seven:
0 = (cycle – time^2)^0.5
(because diameter is the width at value = 0)
Now solve it to “cycle”:
cycle = time^2
With respect to radius = diameter / 2 we must set time = (max_time) / 2. Note: (max_time ) / 2 = radius. For weekdays 7/2:
cycle = radius^2
Additionally, one must shift the function right into – radius to the right:
value_cyc = (radius^2 – (radius – time)^2)^0.5
Now let´s take a look at the function “value_cyc” for seven weekdays 1 to 7 (red). To compare it with the mentioned sine-approach the function (blue)
value_sin = sin(2π*time/14)*3.5
is added:
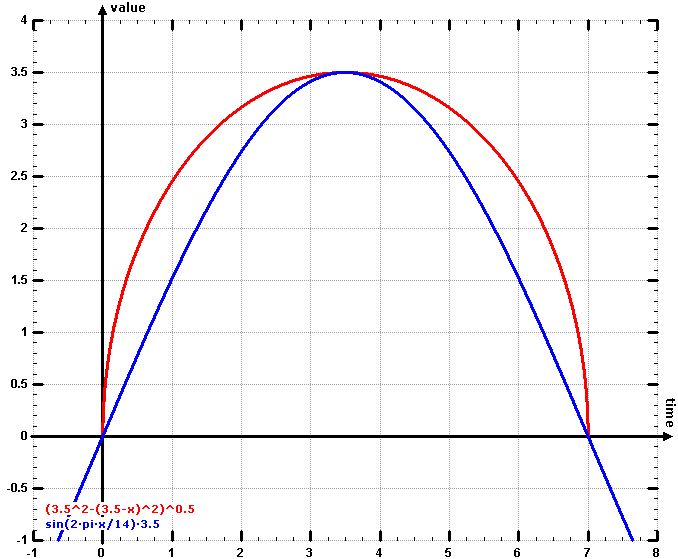
figure created by wzgrapher
The difference is the slope. The function “value_cyc” starts with a stronger increase which leads to higher values at the start and at the end of the period. This effect makes the outcome around the center of the period similar and differentiates the center even more pronounced from the start and the end – compared to “value_sin”.
Note that making data cyclical is not always a good idea. Be careful if the periods not have the same length (e.g. month-days)!
