Previous Relevant Posts
- Single regression with R to identify relationship between WTI and s…
- Getting stock volatility in R & Getting Histogram of returns
What is CAPM?
According to the investopedia (http://www.investopedia.com/terms/c/capm.asp),

The general idea behind CAPM is that investors need to be compensated in two ways: time value of money and risk. The time value of money is represented by the risk-free (rf) rate in the formula and compensates the investors for placing money in any investment over a period of time. The other half of the formula represents risk and calculates the amount of compensation the investor needs for taking on additional risk. This is calculated by taking a risk measure (beta) that compares the returns of the asset to the market over a period of time and to the market premium (Rm-Rf).
How do we approach
Generally, rf is consistent with the T-bill rate. During 2015, it was almost 0.02 (2%) as Fed kept interest rate low to boost the economy. CAPM can be represented in portfolio. Now, I am going to choose the TOP 20 NYSE technology stocks during Mar 2016. This is done by single regression as we used in previous post.
 |
| http://themarketmogul.com/wp-content/uploads/2015/05/Screen-Shot-20… |
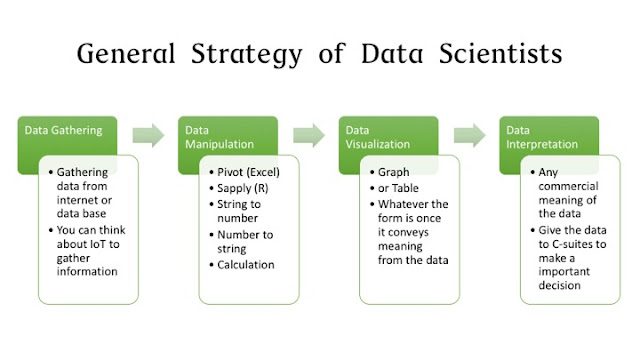
Strategy
(1) Data Gathering: We are going to gather the market data from the API.
(2) Data Manipulation: We choose only Top 20 firms in terms of market cap.
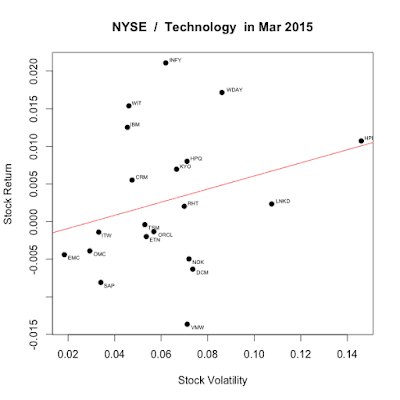
(3) Data Visulaization: Draw the risk-return graph
(4) Data Interpretation: See this graph is consistent with CAPM theory.
Codes
#Getting TOP 100 stocks in NYSE volitility and return
library(TTR) #To get tickers
library(plyr) #For sorting
library(tseries) #For volatility / return
library(stringr) #String manipulation
library(calibrate) #To represent stock name on scatter plot
#NASDAQ, NYSE
market <- “NYSE”
#Technology, Finance, Energy, Consumer Services, Transportation, Capital Goods, Health Care, Basic Industries
sector <- “Technology”
getcapm <- function(stock) {
#Getting data from server
data <- get.hist.quote(stock, #Tick mark
start=”2016-03-01″, #Start date YYYY-MM-DD
end=”2016-03-31″ #End date YYYY-MM-DD
)
#We only take into account “Closing price”, the price when the market closes
yesterdayprice <- data$Close
#This is a unique feature of R better than Excel
#I need to calculate everyday return
#The stock return is defined as (today price – yesterday price)/today price
todayprice <- lag(yesterdayprice)
#ret <- log(lag(price)) – log(price)
rets <- (todayprice – yesterdayprice)/todayprice
#Annualized and percentage
vol <- sd(rets) * sqrt(length(todayprice))
#Getting Geometric Mean.
#You might be tempted to use just mean(). Don’t do that in stock market.
geometric_mean_return_prep <- rets + 1
geometric_mean_return_prep <- data.frame(Date=time(geometric_mean_return_prep), geometric_mean_return_prep, check.names=FALSE, row.names=NULL)
geometric_mean_return = 1
for(i in 1:length(geometric_mean_return_prep)) {
geometric_mean_return = geometric_mean_return * geometric_mean_return_prep[i,2]
}
geometric_mean_return <- geometric_mean_return^(1/length(geometric_mean_return_prep))
geometric_mean_return <- geometric_mean_return -1
information <- c(geometric_mean_return, vol) #It’s a trick to return multiple values in one return.
return(information)
}
convert_marketcap <- function(str) {
str <- gsub(“\\$”, “”, str) #Get rid of “$” first
#The reason why I use \\ is that $ has a special meaning in regular expression
#Regular expression is not the topic. #I’ll deal with later
multiplier <- str_sub(str,-1,-1) #Million? Billion?
pure_number <- as.numeric(gsub(“(B|M)”, “”, str)) #Get rid of M or B. Turn it into number
if(multiplier == “B”) {
#Billion
adjustment <- 1000000000
} else if(multiplier == “M”) {
#Million
adjustment <- 1000000
} else {
#Don’t adjust it.
adjustment <- 1
}
return (pure_number * adjustment)
}
original <- stockSymbols()
#Getting NASDAQ
listings <- original[original$Exchange==market,]
#As these data include “NA,” we need to clean them up for further data manipulation.
#If you don’t clean up NA, you would encounter error while manipulating
listings <- listings[!is.na(listings$MarketCap),]
listings <- listings[!is.na(listings$Sector),]
#I want to focus on the specific sector
listings <- listings[listings$Sector==sector,]
#Market cap is string right now. We need to convert this to number
listings$MarketCap <- sapply(listings$MarketCap, convert_marketcap)
#Sort the list descending order of market capital
listings <- arrange(listings, desc(listings$MarketCap))
capm <- data.frame(ticker=””, volatility=1:20, geometric_return=1:20)
capm$ticker <- listings$Symbol[1:20]
for(i in 1:20) {
information_on_stock <- getcapm(capm$ticker[i])
capm$geometric_return[i] <- information_on_stock[1]
capm$volatility[i] <- information_on_stock[2]
}
main_name <- paste(market, ” / “)
main_name <- paste(main_name, sector)
main_name <- paste(main_name, ” in Mar 2015″)
capm_regression<-lm(capm$geometric_return ~ capm$volatility)
plot(x=capm$volatility,y=capm$geometric_return,pch=19, main = main_name, xlab=”Stock Volatility”, ylab=”Stock Return”)
#I want to know which stock is outlier.
textxy(capm$volatility, capm$geometric_return, capm$ticker)
abline(capm_regression, col=”red”) # regression line (y~x)
print(summary(capm_regression))
Outcome Interpretation
So, thus remaining things are two – Alpha and Beta.