We have a once in a lifetime opportunity to address one of modern society’s biggest challenges – the choice between healthcare or the economy. For the past several decades, we have treated this as an “either or” choice between one or the other; that to improve the economy we must reduce healthcare spending or to improve healthcare we must sacrifice the economy. To that sort of thinking I say BULL!
The coronavirus COVID-19 situation is showing us a very important lesson – that healthcare and the economy are tightly linked; that it can’t be an “either or” choice. As a society – as a world – we must start thinking more holistically about the healthcare or economy challenge and reframe our approach from a scarcity (“either or”) mentality to an abundance (”and”) mentality.
But how do we do that? From where can we draw historical lessons that can guide us in what may be the ultimate society transformation? The good news is that the automobile industry went through a similar challenge. So, let’s see what we can learn from the trials and tribulations of their transformational journey.
Automobile Industry Challenge: Mileage Efficiency or Power
The Arab Oil Embargo of 1973 and 1974 drove the US Government to mandate that the automobile industry achieve an average 27.5 MPG across the fleet of cars that they sold by 1985. The economic realities were that automobile manufacturers started to manufacture cars that traded off horsepower for fuel efficiency. The result was a distinct Economic Value Curve reflecting the nature of that power versus fuel efficiency tradeoff (see Figure 1).
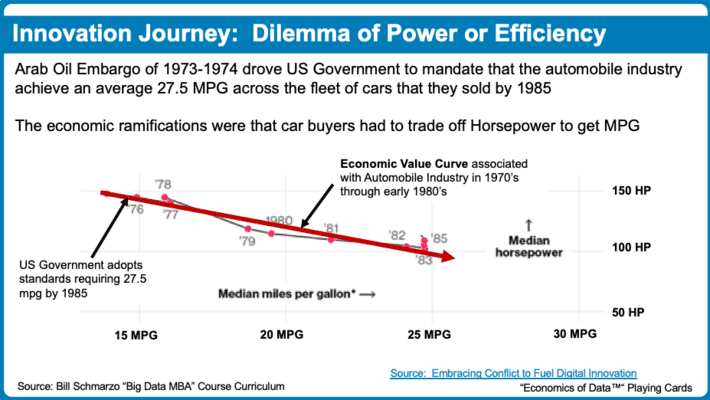
Figure 1: Dilemma of Power or Efficiency Economic Tradeoff
Lesson Learned: A global shock to the existing economic system forced companies and consumers to make an “either-or” tradeoff decision between power versus fuel efficiency; the global shock forced both companies and consumers to confront a tradeoff that pleased no one given the existing economic value curve.
Automobile Industry Transformation: Period of Turmoil
Then, in the mid 1980’s, with the government and society pressure for even more improved fuel efficiency (culminating in new energy legislation signed by George Bush in 1985 that mandated automotive mileage of 35 mpg by 2020), the industry went through a period of exploration, testing, turmoil, failure (remember the Wankel engine?) and learning.
Automobile manufacturers embraced the challenge and ended up both increasing fuel mileage and horsepower. However, this transformation wasn’t due to one big cure all (vaccine). Instead it was through a multitude of smaller product design, development and manufacturing innovations that the transformation was being driven.
These innovations included:
- Use of lighter weight alloys to reduce weight
- Use of turbo-charging and super-charging
- Use of small displacement high-compression engines
- Advancements in diesel engines
- More valves per cylinder
- Cylinder deactivation
- Improved aerodynamics

Figure 2: Automobile Industry Period of Turmoil…and Innovation
Lesson Learned: It wasn’t one big cure all development that drove the automobile industry transformation. It was through a series of smaller product design and manufacturing improvements that compounded to drive the transformation.
Remember, a 1% improvement compounded 365 times yields a 37.78x (times) improvement!
Automobile Industry Transformation: The New Economic Value Curve
By 2007, the automobile industry had achieved something that no one could have even imagined, the ability to provide both power and fuel efficiency. The automobile industry looked at what many automobile executives thought to be a “death sentence” mandate, and emerged a stronger, more viable and more relevant industry. And in the process, transformed the very nature of the automobile industry’s economic value curve (see Figure 3).
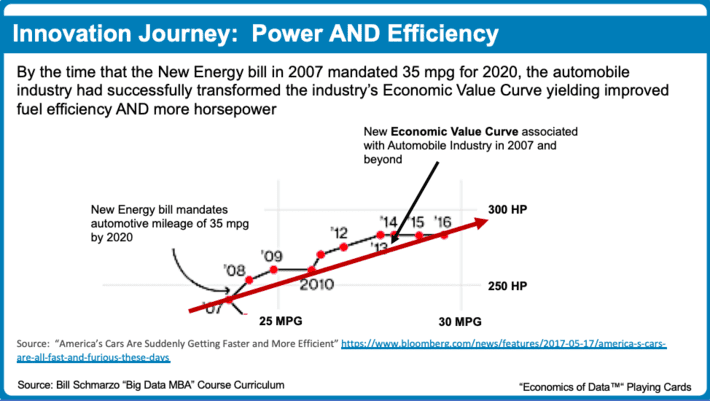
Figure 3: The Transformation of the Automobile Industry Economic Value Curve
Lesson Learned: Don’t count out the power of human innovative thinking driven through collaboration and a mentality that all ideas are worthy of consideration.
Summary
Now is not the time to run scared.
Now is not the time to just hunker down and wait this out.
Now is the time to act and to take advantage of the COVID-19 crisis and challenge the scarcity mentality that forces us into the healthcare versus the economy tradeoff. Now is time to take the lessons learned from the automobile industry and start exploring, test, failing and learning about how we can deliver world class healthcare AND drive robust economic growth.
And it won’t be a one-cure-all vaccine that fixes this problem, because the next COVID-19 type problem is just around the healthcare corner. It will be through a multitude of small, 1% improvements that will drive us to that 37x improvement in both healthcare and economic growth. It will be little improvements in remote testing, universal diagnostics, universal data sharing and transparency, personal hygiene, healthy lifestyle choices, healthcare education, and universal data sharing, transparency and the sharing of analytic insights.
Let’s do this today:
- Embrace, not avoid, diversity of ideas and perspectives.
- Understand that all ideas are worthy of consideration, maybe even from the most unlikely of sources.
- Nurture the power of collaborative thinking and the power of standing on each other’s shoulders.
- Don’t wait for the big bang solution (vaccine), but instead make a series of marginal improvements that gradually evolve the supporting infrastructure and ecosystem.
- And finally, exploit the magic of compounding; that a 1% improvement compounded 365 times yields a 38x (times) improvement!
I’m up to the challenge. How about you?
