An interesting application of Benford’s and Zipf’s Laws to fraudulent Covid-19 data was published recently on the peer-reviewed PLOS-ONE website. The study, titled On the authenticity of COVID-19 case figures [1] showed how the two laws could be used to identify fraudulent Covid-19 data.
The “Usual” Applications of Benford’s and Zipf’s Laws
- Benford’s law [no term] is a probability distribution [no term] for the likelihood of the first digit in a set of numbers [2]. The idea is that there are set probabilities for certain numbers (1, 2, 3,…) occurring in certain lists of numbers. The probability of any particular number occurring is given by a formula:
 As well as the fairly mundane application of analyzing data in written texts like The Times or Reader’s Digest, it can be applied to analyze large sets of naturally occurring numbers like stock market prices, income distributions, or river drainage rates.
As well as the fairly mundane application of analyzing data in written texts like The Times or Reader’s Digest, it can be applied to analyze large sets of naturally occurring numbers like stock market prices, income distributions, or river drainage rates. - Zipf’s law, which gives rise to the Zeta probability distribution, [no term] states that, given a list of the most frequent words in a random book, the most common word will appear twice as often as the second most common, which will appear twice as often as the third most common, and so on. Practical applications include analysis of data that has large steps down from the top, like the drop from executive salaries to management salaries or the number of books ales by top authors (like Stephen King or J.K. Rowling) compared to lesser know authors.
Interestingly, both distributions can also be employed to detect fraud. Benford’s law detects the probability of a particular number appearing first, so any large set of numbers should follow set probabilities. If fraudsters are constantly inflating figures (e.g. increasing their average bill from $100 to $900), the data set will upset the natural order of data– violating Benford’s law and producing an anomaly that can be picked up by an algorithm. The law has a long history of detecting both financial and non-financial fraud, including electoral fraud [3], scientific fraud [4], and fake law enforcement statistics [5]. Kennedy and Yam, the authors of this new study took an unusual step forward and applied Zipf’s law (in addition to Benford’s) to finding fraud in published Covid-19 data.
Fraud in Covid-19 Data
In the early days of the pandemic, it was difficult (if not impossible) to ascertain how serious the Covid-19 outbreak actually was. For example, Chinese authorities downplayed the outbreak’s threat, allowing countless numbers of carriers to travel globally [6]. But how can we be certain that the case numbers coming out of China (and indeed, every other country) were fraudulent? Were countries deliberately dampening figures in order to keep tourism alive? One way to answer these questions is to apply the two abovementioned laws to the data, and see if any anomalies crop up. This is exactly what Kennedy and Yam did in their study.
One of the questions the authors tried to address is that when they found fraudulent data, did it come from a central government or local authorities feeding incorrect data to the top? The authors found that Zipf’s law can help answer this question: significant deviations from Zipf’s law might indicate fraud by figures reported by a central government. However, if a country’s figures largely follow Zipf’s law with a few deviations on the sub-national level, that might indicate fraud by regional authorities.
The authors also noted that during the early days of an epidemic, where there are few cases per capita, the number of confirmed cases seems to obey Benford’s law to a “large degree.” This gives a very simple and practical way to ascertain whether reported numbers of cases in any pandemic–especially in the early days–are likely to be fraudulent.
Applying these laws and identifying which data is false and which is true can result in a much faster, better response to future pandemics. It’s worth noting though that at this stage the study’s result are purely theoretical as they have been applied to the current Covid-19 pandemic, which has resulted in government action on an unprecedented scale. Further study of past and future pandemics is necessary to confirm the validity of applying these statistical laws the data from pandemics.
References
[1] On the authenticity of COVID-19 case figures
[2] Frunza, M. (2015). Solving Modern Crime in Financial Markets: Analytics and Case Studies. Academic Press.
[3] Klimek P, Jiménez R, Hidalgo M, Hinteregger A, Thurner S. Forensic analysis of Turkish elections in 2017-2018. PLOS ONE. 2018;13(10). pmid:30289899
[4] Diekmann A. Not the first digit! Using Benford’s law to detect fraudulent scientific data. Journal of Applied Statistics. 2007;34(3):321–329.
[5] Deckert J, Myagkov M, Ordeshook PC. Benford’s law and the detection of election fraud. Political Analysis. 2011;19(3):245–268.
[6] 8 times world leaders downplayed the coronavirus and put their coun…
Covid-19 image: CDC (Public Domain).

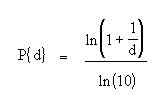 As well as the fairly mundane application of analyzing data in written texts like The Times or Reader’s Digest, it can be applied to analyze large sets of naturally occurring numbers like stock market prices, income distributions, or river drainage rates.
As well as the fairly mundane application of analyzing data in written texts like The Times or Reader’s Digest, it can be applied to analyze large sets of naturally occurring numbers like stock market prices, income distributions, or river drainage rates.