Imagine that one day, you see people are queuing up in front of Bank A; so you ask the staff at the counter, you are told that they are offering anyone (regardless of their credit history) a loan of $100,000 at a fixed annual rate at 2%. You then look around, the Bank B next door offers 1-year term deposit with a fixed annual rate at 3% for the same amount ($100,000). After 5 minutes’ waiting, you sign for the loan from Bank A and immediately, you deposit the borrowed $100,000 in Bank B, expecting to earn 1,000 dollar based on (3%-2%) x 100,000 one year from now. Your lucky day!
In Finance, without investments, an opportunity that allows one to gain profits from simultaneously buying and selling something is called Arbitrage Opportunity. The above opportunity, which involves borrowing through a loan from Bank A and lending through a deposit at Bank B, represents an arbitrage opportunity in financial economists’ parlance. However, one can easily see this type of opportunities won’t last long. In efficient markets, according to Nobel Laureate economist Eugene Fama, such arbitrage opportunity should not exist and could never last. However, in our paper titled Arbitrage opportunities in CDS Term Structure: Theory and Implications on OTC Derivatives, we found that the contrary is true at least in the credit default swap market (to be explained below).
In this study, we applied calculus, probability theory and economic principles to derive so-called No-arbitrage conditions, which basically sets out the basic relationship that should be followed by CDS contracts of different maturities should follow. Violating the conditions we derived, nonsensical probability (negative or greater-than-1 probability) and arbitrage opportunities will emerge. Based on the mathematical conditions derived in our research paper, after examining 30+ million CDS contracts, we identified 2,416 pairs of CDS contracts as arbitrage opportunities, which are not supposed to exist. Is the Nobel Laureate wrong or are there other reasons that deter investors from queuing up to take advantage of such opportunities?
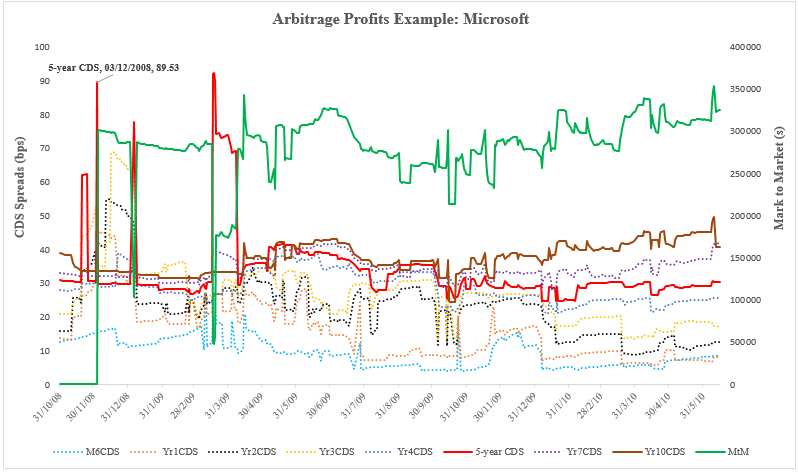
CDS is basically tradable insurance contract that provides the buyer the recovery of pre-specified losses as the result of the reference name. It is slightly more complicated than the loan in the example above; however, the principle of arbitrage works exactly the same. Here is an example from two CDS contracts selling CDS protection against default of Microsoft (Please read the paper for more details.). The green line indicates the value of the trades. On 03/12/2008 (Please note that the notorious Lehman Brothers just defaulted 3 months earlier on 15/09/2008; it’s the prime of the financial crisis.), the green line starts at zero, indicating that no investment is needed; also, throughout the time, it is above zero, which means positive profits persist for the trades, thus, an arbitrage opportunity. Further details are in the paper: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3282399