Here I want to present my new book on advanced algorithms for data-intensive applications named “Probabilistic Data Structures and Algorithms in Big Data Applications” (ISBN: 9783748190486). The detailed information about the book you can find at its webpage and below I give you some introduction to the topic this book is about.
What are the probabilistic data structures and why do we need them?
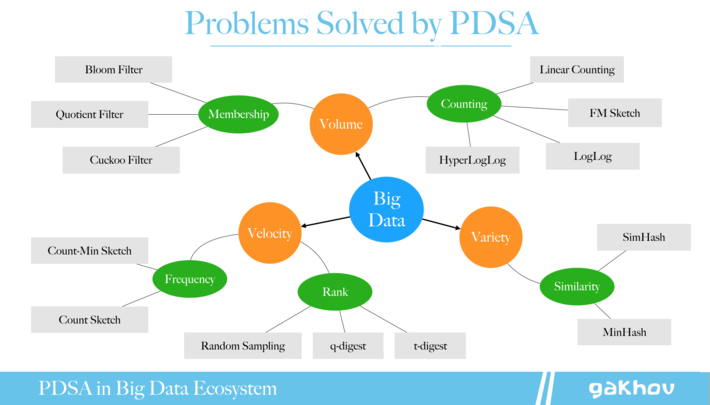
There is no doubt that a lot of data creates unbelievable opportunities to learn and opens new horizons for business. However, this also implies lots of technical challenges. I guess, everyone heard about Volume, Velocity, and Variety, The Three V’s of Big Data. These dimensions imply such problems as efficient membership querying, cardinality estimation, frequency and rank computation for data streams, and similarity calculation.
Many of these problems can be solved with parallel computation including usage of the MapReduce paradigm and such popular frameworks for distributed processing as Apache Hadoop, Apache Spark, Apache Flink, Apache Storm, and others.
However, at some point, the amount of data (or its frequency, or variety, or all together) rises so high that we cannot scale up anymore our system, regardless the amount of money and resources we have. Thus, we have to agree to lost some data in order to be able to continue learning. There are two main approaches in this case – Sampling and Hashing.
Sampling
- Process subset of elements
- Discard rest
- Use existing setup and algorithms
- Interpolate results
Hashing
- Process all elements
- Compression with information loss
- Use advanced algorithms
- Approximate results
This book is about Probabilistic Data Structures and Algorithms (PDSA) that based on hashing and heavily use various pattern observation techniques to provide approximate results even under heavy input compression that lead to information loss. Such data structures have a strong theory behind and provide reliable ways to estimate possible errors which fully compensated for by extremely low memory requirements, constant query time, and scaling.
They are not necessarily new. Probably, everybody knows about the Bloom filter data structure, designed in the 70s, it efficiently solves the problem of performing membership queries (a task to decide whether some element belongs to the dataset or not) in a constant time without requirements to store all elements. This is an example of a probabilistic data structure, but there are much more that have been designed for various tasks in many domains.
Such data structures already implemented in many popular and well-known products such as Google Big Query, Amazon Redshift, Redis, Cassandra, CouchDB, Elasticsearch, and many others. For instance, you can use `approx_count_distinct` command in Spark SQL or `PFCOUNT` in Redis that actually powered by the HyperLogLog algorithm, another example of PDSA.

Organization of the book
This book consists of six chapters, each preceded by an introduction and followed by a brief summary and bibliography for further reading relating to that chapter. Every chapter is dedicated to one particular problem in Big Data applications, it starts with an in-depth explanation of the problem and follows by introducing data structures and algorithms that can be used to solve it efficiently.
The first chapter gives a brief overview of popular hash functions and hash tables that are widely used in probabilistic data structures. Chapter 2 is devoted to approximate membership queries, the most well-known use case of such structures. In chapter 3 data structures that help to estimate the number of unique elements are discussed. Chapters 4 and 5 are dedicated to important frequency- and rank-related metrics computations in streaming applications. Chapter 6 consists of data structures and algorithms to solve similarity problems, particularly — the nearest neighbor search.

In case if you want to reach me, connect at Twitter @gakhov or visit the webpage of the book at https://pdsa.gakhov.com
