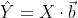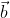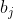Machine Learning with C++ – Polynomial Regression (CPU)

There are a lot of articles about how to use Python for solving Machine Learning problems, with this article I start series of materials on how to use modern C++ for solving same problems and which libraries can be used. I assume that readers are already familiar with Machine Learning concepts and will concentrate on programming issues only.

The first part is about creating Polynomial Regression model with XTensor library. This is C++ library for numerical analysis with multi-dimensional array expressions, and containers of XTensor are inspired by NumPy. A lot of functions in this library also have semantic similar to NumPy.so should be easier to start with this library rather then with Eigen or ViennaCL if you already familiar with NumPy.

I start with simple polynomial regression to make a model to predict an amount of traffic passed through the system at some time point. Our prediction will be based on data gathered over some time period. The X data values correspond to time points and Y data values correspond to time points.

For this tutorial I chose XTensor library.This library was chosen because of its API, which is made similar to numpy as much as possible. There are a lot of other linear algebra libraries for C++ like Eigen or VieanCL but this one allows you to convert numpy samples to C++ with a minimum effort.

0. Short polynomial regression definition Polynomial regression is a form of linear regression in which the relationship between the independent variable x and the dependent variable y is modeled as an n-th degree polynomial in x.

   

   Because our training data consist of multiple samples we can rewrite this relation in matrix form:

   

   Where

   

   and k is a number of samples if the training data. So the goal is to estimate the parameters vector . In this tutorial I will use gradient descent for this task. First let’s define a cost function:

   

   Where Y is vector of values from our training data. Next we should take a partial derivatives with respect to each  term of polynomial:

   

   Or in the matrix form:

   

   And use these derivatives to update vector  on each learning step:

   

   Where l is a learning rate.

Continue reading the article and source code here. Please feel free to leave comment or create issue in repository if you find some mistakes.