Introduction
In a regular neural network, the input is transformed through a series of hidden layers having multiple neurons. Each neuron is connected to all the neurons in the previous and the following layers. This arrangement is called a fully connected layer and the last layer is the output layer. In Computer Vision applications where the input is an image, we use convolutional neural network because the regular fully connected neural networks don’t work well. This is because if each pixel of the image is an input then as we add more layers the amount of parameters increases exponentially.
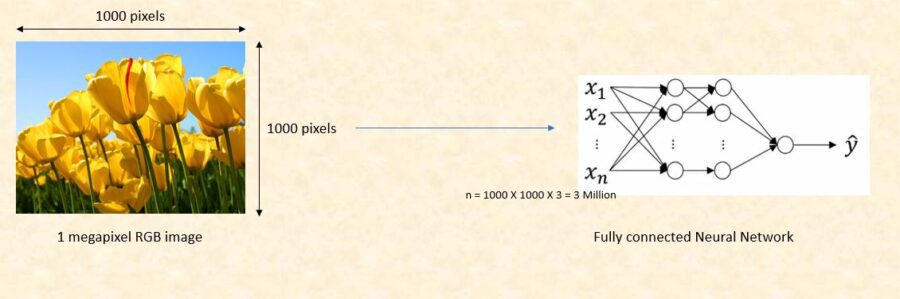
Consider an example where we are using a three color channel image with size 1 megapixel (1000 height X 1000 width) then our input will have 1000 X 1000 X 3 (3 Million) features. If we use a fully connected hidden layer with 1000 hidden units then the weight matrix will have 3 Billion (3 Million X 1000) parameters. So, the regular neural network is not scalable for image classification as processing such a large input is computationally very expensive and not feasible. The other challenge is that a large number of parameters can lead to over-fitting. However, when it comes to images, there seems to be little correlation between two closely situated individual pixels. This leads to the idea of convolution.
What is Convolution?
Convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it [1]. In a neural network, we will perform the convolution operation on the input image matrix to reduce its shape. In below example, we are convolving a 6 x 6 grayscale image with a 3 x 3 matrix called filter or kernel to produce a 4 x 4 matrix. First, we will take the dot product between the filter and the first 9 elements of the image matrix and fill the output matrix. Then we will slide the filter by one square over the image from left to right, from top to bottom and perform the same calculation. Finally, we will produce a two-dimensional activation map that gives the responses of that filter at every spatial position of input image matrix.
Challenges with Convolution
1- Shrinking output
One of the big challenges with convolving is that our image will continuously shrink if we perform convolutional operations in multiple layers. Let’s say if we have 100 hidden layers in our deep neural network and we perform convolution operation in every layer than our image size will shrink a little bit after each convolutional layer.
2- Data lost from the image corners
The second downside is that the pixels from the corner of the image will be used in few outputs only whereas the middle region pixels contribute more so we lose data from the corners of our original image. For example, the upper left corner pixel is involved in only one of the output but middle pixel contributed in at least 9 outputs.
Read the full article at engmrk.com
