Bayesian Machine Learning (part -5)
Introduction: Expectation-Maximization
In this blog we are going to see how Expectation-maximization algorithm works very closely. This blog is in strict continuation of the previous blog. Previously we saw how probabilistic clustering ended up into chicken-egg problem. That is, if we have distribution of latent variable, we can compute the parameters of the clusters and vice-versa. To understand how the entire approach works we need to learn few mathematical tools, namely : Jensen’s inequality and KL divergence.
So, let’s start!!!
Jensen’s Inequality
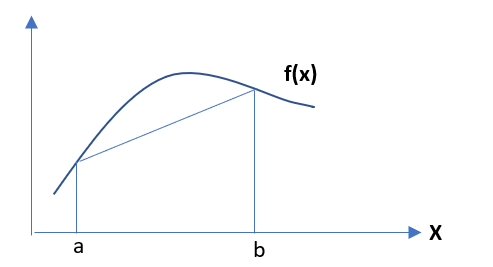
Jensen’s inequality states that, for a convex function f(x) , if we select points as x = a and x = b, also we take α,β such that α + β = 1 ,then
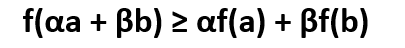
If we consider x as a random variable and it takes the values a, b with probability α, β (as we know α + β = 1)., then the expression αa + βb is the expectation of x –> E(x), and the expression αf(a) + βf(b) — > is E(f(x)). Thus, the expression of Jensen’s inequality can be re-written as:
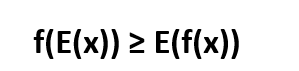
This above expression will be used in further analysis.
Kullback–Leibler divergence
This is the method of computation of divergence between two probability distribution functions. The mathematical expression is as follows:
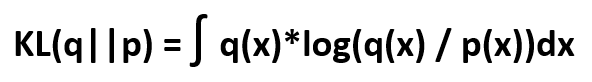
Where q(x) and p(x) are pdf. functions on a random variable x. KL(q||p) is always ≥ 0.
Expectation – Maximization Algorithm
Now from our previous blog discussion, we know that marginalized posterior distribution is as follows :
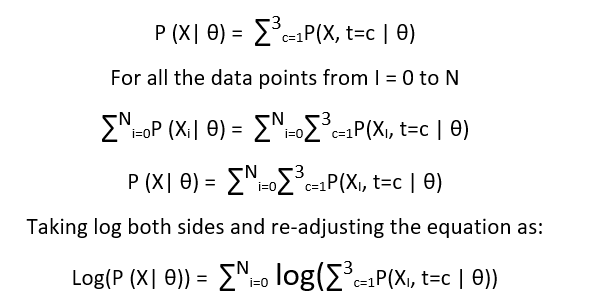
Now we need to maximize the above expression w.r.t θ. The problem here is that maximization of the above expression is not simple, and function usually has many local maxima. We can use gradient – decent here but the process will become too lengthy. To solve this, we use a different approach here all together. We will try and construct a lower bound of the above expression. We will use Jensen’s inequality. And once we build our lower bound, we will try and maximize it.
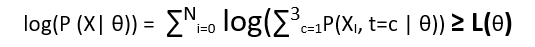
the lower bound is also called variational lower bound
here we will try to apply Jensen’s inequality to compute the lower bound
consider the log as our function f and let us introduce a new function q(t=c, θ), and multiply it in denominator and numerator. So the new equation looks like:
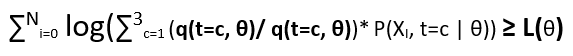
Now consider the ratio (P(XI, t=c | θ)/ q(t=c, θ)) as random variable and q(t=c, θ) as the probabilistic coefficient as ∑3c=1 q(t=c, θ) = 1
Now from Jensen’s inequality, we know that:
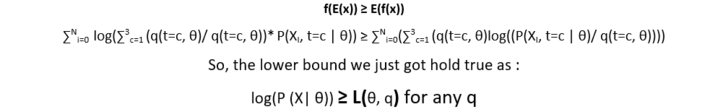
Graphically
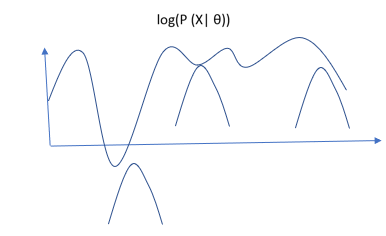
All the above small curves are the family from lower bound L(θ, q).
Expectation Step
So, one thing is clear that Lower bound will always be beneath the actual function, and we need to maximize the lower bound to be as much closer to actual function as possible. In expectation step we fix our θ and try to maximize the lower bound. We do it by reducing the gap between actual function and the lower bound. The equation is as follows :

putting in some linear algebra, the equation ends up in the expression of KL divergence between q and posterior t
the solution of expectation step is :
q(t=c) = P(t=c | Xi ., θ)
Maximization step
Once we get the gap reduced between the variational lower function L(θ, q) and log(P(X |θ)), we maximize our lower bound function w.r.t θ.
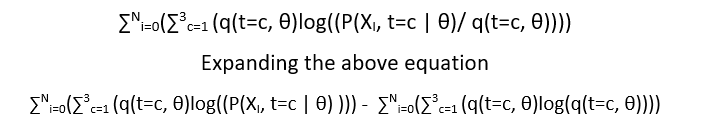
The second component of above equation is const. w.r.t θ. Therefore, we drop it, the new equation remains is:

In the next post we will continue our discussion with Gaussian mixture model and try to implement Expectation – Maximization algorithm to perform clustering.
Thanks for reading !!!
