Today I would like to share some of the elements I covered as part of the Data Science for Internet of Things courseat the Department of Continued Education of the University of Oxford. Thanks to Ajit Jaokar, I covered two topics for this course: anomaly detection for time series and predictive maintenance. And I would like to thank him for the review of this blog post.
This blog post will be about anomaly detection for time series, and I will cover predictive maintenance in another post.
Challenges
When starting research for the course, the main goal was to cover anomaly detection in an Internet of Things context.
To put it in a different way, this simply means that we have to look for anomalies in spatio temporal datasets which can be summed up in those different types of data:
- time series,
- stream data,
- spatio temporal data,
- etc.
This classification is directly taken from slides presented at SDM 2013 by Gupta and al. See this link.
I decided to focus on time series, since that would take already enough time to cover, even without going into the details.
Surprisingly, while there are packages in some languages to cover forecasting and anomaly detection on time series, there is not a lot of research of methodology materials related to anomaly detection on time series in a broad context.
Thus, the main challenge for building the course was to find / build materials that would be broad enough to create the course.
Materials
Beyond the slides from SDM 2013 mentioned previously, there are some specific elements that have been written such as (list is not exhaustive):
- Twitter anomaly detection method (based on Seasonal Hybrid Extreme Studentized Deviate Test, i.e. S-H-ESD which builds upon Generalized ESD Test) and its associated R package. See this link for more information.
- Rob J. Hynman and al. R package for unusual time series detection and associated working paper. See here and here for more information
- Ted Dunning and Ellen Friedman short ebook: Practical Machine Learning: A New Look at Anomaly Detection.
- Some Netflix blog post. Sadly, they are not accessible anymore, while still linked by Google.
However, the two main sources of information that I found the most useful with regards to the topic covered were:
Anomaly Detection of Time Series, by Deepthi Cheboli, University of Minnesota, 2010.
Anomaly Detection: a survey, by Chandola and al. ACM Computing Surveys, 2009.
Those papers were the two main sources of information for me to write the course, since they are both comprehensive enough to cover a wide range of techniques.
In the first paper by D. Cheboli, the focus is exclusively on Time Series which fits the course quite well. It also has the advantage of providing a framework for analysing time series with the goal of anomaly detection in mind.
The second paper by Chandola and al. is a comprehensive overview of anomaly detection techniques, whether they are related to temporal data or not.
Types of anomalies
Anomalies in Time Series can be grouped in four categories:
- point anomalies: a single point in a Time Series is anomalous compared to the rest of the data
- contextual anomalies: a data instance in a Time Series which is considered anomalous because of the context (for instance, low temperatures in summer in the northern hemisphere). In order to detect such anomalies, we need to have information on the context itself.
- subsequence anomalies: these are collective anomalies which are anomalous with regards to the rest of the data even though data points from the subsequence might not be considered anomalous
- time series anomalies: Time Series which are anomalous with respect to a set (database) of anomalies
The paper from Chandola and al. illustrates very well the complexity of identifying subsequence anomalies with the following figure:
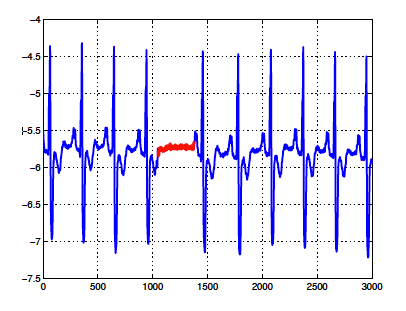In the figure, the anomalous subsequence in red corresponds to a condition called Atrial Premature Contraction which is cardiac dysrhythmia with premature heartbeats in the atria.
The interesting element about this figure is that each point of the red subsequence is not in itself an anomalous point. If we were to look at the average of the red subsequence, it would roughly be equivalent to the average of the blue subsequences.
Problem setting
There are three different types of anomaly detection problems which of course will require different techniques to be addressed:
- unsupervised anomaly detection: this corresponds to the broadest case, where we do not have information about where and if there is an anomaly in the dataset we are exploring.
- semi supervised anomaly detection: in this case, we have a dataset that we know is normal, there is no anomalies within it.
- supervised anomaly detection: this last case is where a dataset is fully labelled with normal and anomalous data elements.
Depending on the type of time series studied, anomaly detection will fall into one of those categories, either because there is not enough information to move from one type to the other (for instance failure data in an industrial context might be rare, so we will mostly have semi supervised problems).
Or we might just want to create clusters of subsequences (for instance in the case of the ECG above) to help in labelling them to build a training database for supervised anomaly detection. This reduces the hassle of exploring the full dataset and labelling all subsequence by hand.
Framework
The goal of the course was to provide a framework that can be applied to any kind of situation with anomaly detection on time series.
The framework I created is based on the elements found in the paper from D. Cheboli and is not much different from the framework that we would use for other kinds of datasets.
It is represented in the following figure:
In essence, this is a four-step process:
- Transforming the time series
- Model the time series
- Conduct the evaluation
- Label and / or review the results
Transforming the time series
The first step (transforming the time series) consists in applying transformation techniques to the time series in order to ease the following steps. In terms of transformation, several possibilities exist depending on the type of data in the time series:
- Fourier transformation or any kind of transformation changing the data from the time domain to the frequency domain
- Aggregation type of transformation with the transformation of a set of consecutive value to a representative value (for instance, the average of a window)
- Alignment between time series to be able to compare time series
- Discretization with the transformation to a discrete sequence of bins
Modelling the time series
The second step (which is probably wrongly named) consists in choosing the techniques to apply to work on anomaly detections for time series. Those techniques fall into five categories:
- window based techniques
- proximity based techniques
- prediction based techniques
- hidden Markov model based techniques
- segmentation based techniques
All those categories are taken from the paper written by D. Cheboli and only the first three were covered during the course.
Evaluating, labelling & reviewing
The last two steps consist in computing the anomaly score of the time series being evaluated.
The anomaly score computation depends on the type of techniques that were used in the previous step. For instance, if the technique used is a proximity based technique to assess a time series with respect to a time series database, the anomaly score can be its distance (using the right distance metric, such as Dynamic Time Warping measure) from the different clusters of time series created from the time series database.
With this anomaly score, we can then rank the different time series (or pieces of it) and assess them or directly classify them if we have previously established thresholds in the modelling phase.
Next steps
With regards to the course, there are definitely elements that need improvements which will be addressed in a later iteration of it as well as in the upcoming book Ajit and I are preparing.
For instance, in the modelling phase, only the first three types of techniques were covered and all will need to be covered. And additional techniques can probably be added.
The transformation section was short on examples and can definitely be improved.
And the last two steps are not as detailed as the previous two, since this is were domain specific knowledge is important. But I will need to add more examples there.
One of the participants came up with an interesting question that I need to explore further: how do we deal with time series with sparse data? I don’t have an answer as of today but this is worth exploring.
Feel free to leave a comment or reach out to jjb at cantab dot net or jjb at datagraphy dot io if you want more information or if you would like to discuss some of the points above. This post is also available here.
