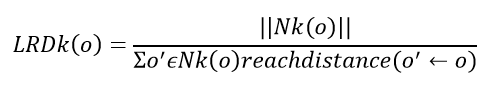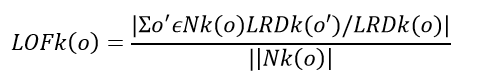Outliers are patterns in data that do not confirm to the expected behavior. While detecting such patterns are of prime importance in Credit Card Fraud, Stock Trading etc. Detecting anomaly or outlier observations are also of importance when training any of the supervised machine learning models. This brings us to two very important questions: concept of a local outlier, and why a local outlier?
In a multivariate dataset where the rows are generated independently from a probability distribution, only using centroid of the data might not alone be sufficient to tag all the outliers. Measures like Mahalanobis distance might be able to identify extreme observations but won’t be able to label all possible outlier observations. The local outlier factor is a density-based outlier detection method derived from DBSCAN; the intuition behind the approach is that the density around an outlier object will be significantly different from the density around its neighbors.
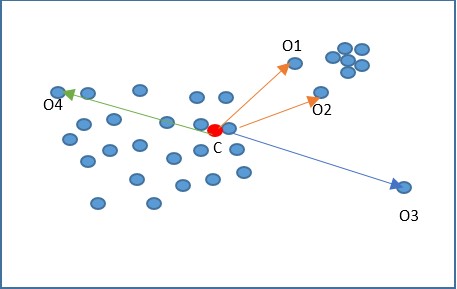
In the figure above, the red dot (C) indicates the center of the data; a distance-based method will only be able to identify o3 and o4 as the outliers, while in reality o3 is an outlier while o4 is not. Also, o1 and o2 are two outlier observations, considering the local neighborhood while based on global data distribution; they are not classified as outliers.
Local outlier factor is a density-based method that relies on k-nearest neighbors. The LOF method scores each data point by computing the ratio of the average of densities of the neighbors to the density of point itself. The steps involved in computing the LOF are as below:
- Calculate distance between the pair of observations.
- Find the kth nearest neighbor observation; calculate the distance between the observation and k-Nearest neighbor.
- Calculate Local Reachability Density (LRD): LRD is the most optimal distance in any direction from the neighbor to the individual point. Mathematically it’s the count of items in k’s nearest neighbor set divided by the max of the kth nearest neighbor of the point and the distance between the point and its adjoining point. The distance is referred as reach distance.

- Local Outlier Factor(LOF) as defined above will be the ratio of local reachability of o and o’s k-nearest neighbors

- The lower is the local reachability of o and the higher the reachability of k nearest neighbors of o higher the LOF.
The LOF value of less than 1 is an indicator that the observation is not an outlier, while a value greater than 1 indicates an outlier. The cut-off can be higher if the data is sparse.
R and python both have implementation of LOF. In R the technique can be implemented using the packages DmWR and Rlof (parallel implementation). Scikit learn in python has the implementation of the algorithm. Below is an illustrative example of LOF technique on a simulated dataset.
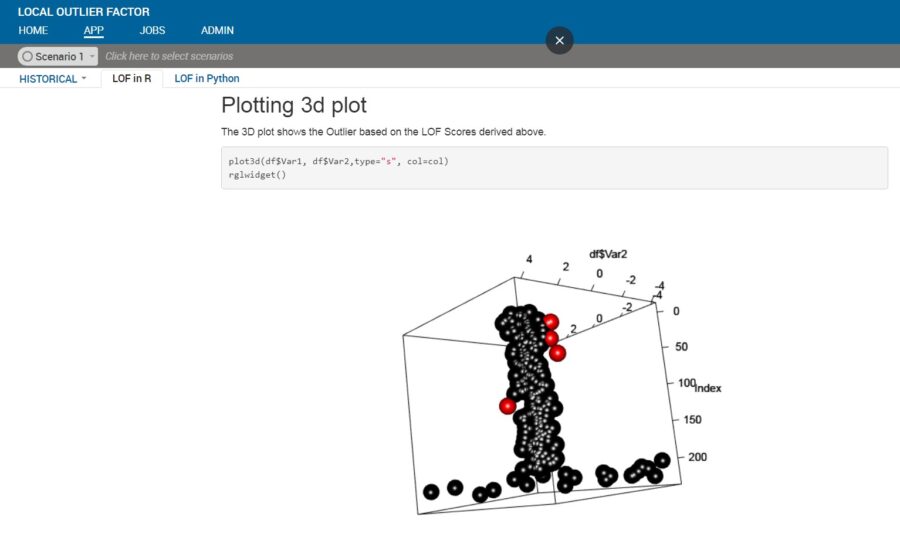
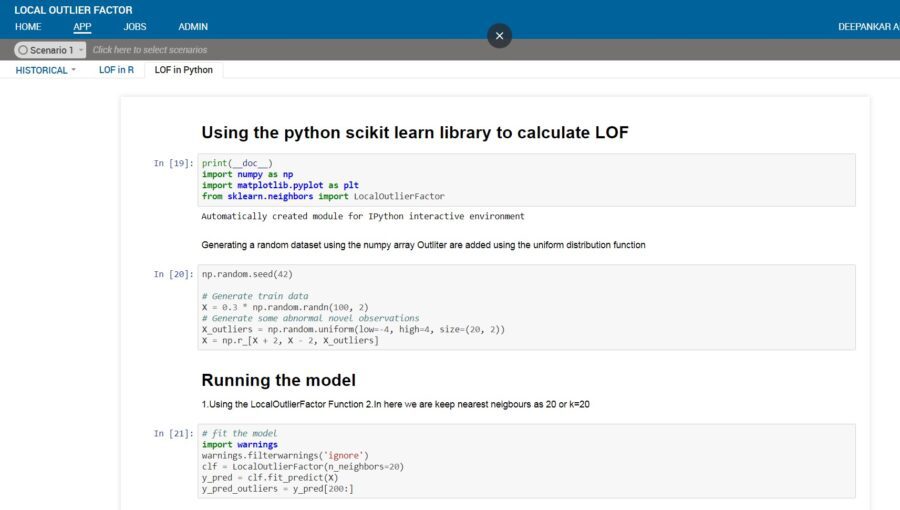
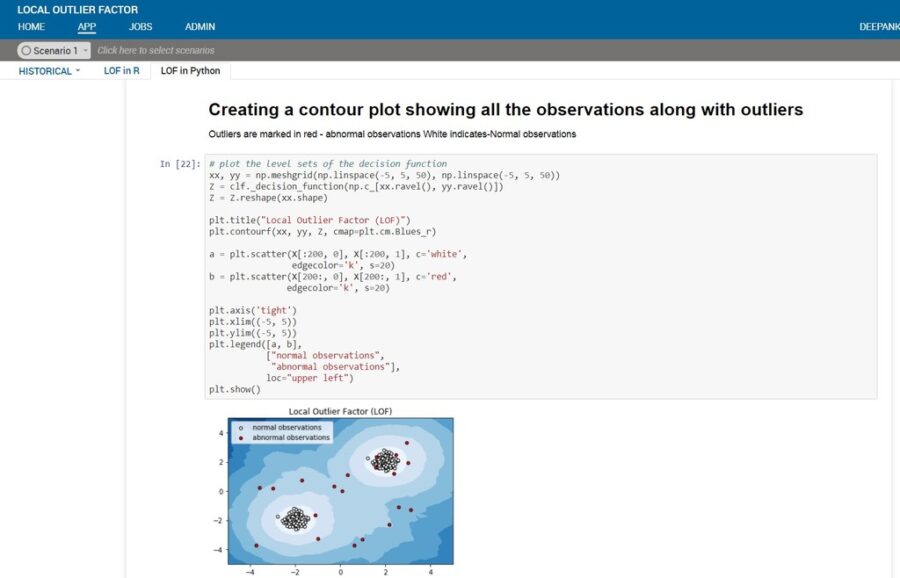
Disadvantage of LOF:
- Scalability is a big issue as the computations are memory-intensive and hence, a good computing infrastructure is required for bigger datasets
- The user needs to provide the input “k”, this input might not be optimal giving incorrect results
Advancements to overcome the disadvantages:
The drawbacks of LOF can be overcome using the some of the latest advancements in algorithms and spark- and Hadoop-based infrastructure. Below are some algorithms that can be looked into from a scalability perspective:
- DILOF: Effective and Memory Efficient Local Outlier Detection in Data streams
- Scalable Top-n local outlier detection: Uses pruning to eliminate most points from the set of potential outlier candidates without computing LOF or even calculating k nearest neighbors.
FICO Xpress Insight offers an excellent platform to develop applications, involving both predictive and prescriptive analytics. To learn more, visit the website https://community.fico.com/s/optimization
References:
- Breunig, M. M., Kriegel, H., Ng, R. T., & Sander, J. (2000).LOF: Identifying Density Based Local Outliers
- Yizhou Yan (Worcester Polytechnic Institute);Lei Cao (Massachusetts Institute of Technology);Elke Rundensteiner (Worcester Polytechnic Institute) Scalable Top-n Local Outlier Detection
- Gyoung S. Na, Donghyun Kim, Hwanjo Yu POSTECH (Pohang University of Science and Technology), South Korea {ngs00, kdh5377, hwanjoyu}@postech.ac.kr. DILOF: Effective and Memory Efficient Local Outlier Detection in Da…