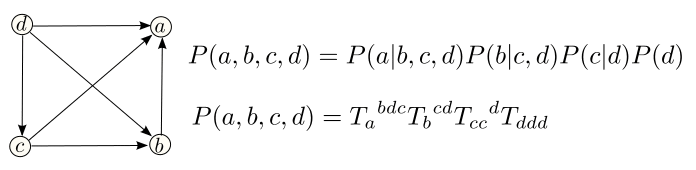
Article Teaser: Tensor networks can be used to denote many physical quantities other than probabilities so they are not tailor made for the job of representing probabilities like Bayesian networks are. Judea Pearl won the Turing prize for his work in Bayesian networks. Hinton, one of the most famous Neural Nets researchers, gives Judea Pearl and his Bayesian networks full credit for motivating the invention of probabilistic AI, which is the natural analogue of quantum AI, except in quantum AI, you replace the probabilities of Probabilistic AI by probability amplitudes. Probabilistic AI software: Probability module of Tensorflow, Pyro extension of Pytorch , PyMC, Stan, Edward, Winbugs, etc., etc.
Tensor Networks (tnets) have a very long and illustrious history in General Relativity and High Energy Physics: t’Hooof and Veltman used them in Diagrammar to study the renormalization of gauge theories, Penrose applied them to General Relativity, Cvitanovic used them in his “Birdtracks” book to study Group Theory.
Quantum circuits are clearly a form of tnet. Quantum circuit diagrams were pioneered by Deutsch, who extended the diagrams used by people (e.g., Toffoli and Bennett) working on classical reversible computation by making those diagrams complex valued instead of real valued, and adding single qubit rotations to the CNOTs and doubly controlled NOTS (aka, Toffoli gates) that were already in use in reversible computation.
Guifre Vidal is often credited with being one of the first to use tnets for quantum computing, although he appears to have started using tnets relatively late in their history. This is his first paper in arxiv, dated 2005, where he uses the term “Tensor Network” in the title
Classical simulation of quantum many-body systems with a tree tensor network, by
Yaoyun Shi, Luming Duan, Guifre Vidal.
The use of tnets in quantum computing software has exploded recently, with the first release on May 2019 by Google of a software library called “TensorNetwork”
https://github.com/google/TensorNetwork
A part of tnet history that is never mentioned by the writers and users of Google’s tnet software is its strong connection to a much deeper tool, Quantum Bayesian Networks (qbnets). Just like in General Relativity, where tensor notation can be replaced by the far more geometric language of differential forms, in quantum computing, tensor notation can be replaced by the far deeper language of qbnets. Why deeper? Briefly put, unlike tnets, qbnets are a natural generalization to quantum mechanics of classical bayesian nets. Thus, unlike tnets, qbnets are directly relatable to a rich vein of advances, dating back many decades, by Bayesian network pioneers like Judea Pearl and hierachical model pioneers like Andrew Gelman, and to an equally rich vein of software for Bayesian Networks, hierarchical models, MCMC, etc., such as WinBugs, Stan, Edward, PyMC, Tensorflow’s Probability module, PyTorch’s Pyro extension, etc. I’m afraid that the quantum tnet community is ignoring its precursors and taking credit for inventing the wheel.
Original post can be viewed here.
