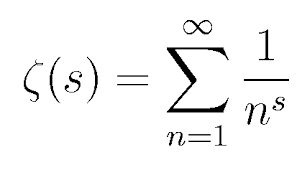
The Riemann Hypothesis is arguably the most important unsolved problem in mathematics. It falls into an area called Analytic Number Theory which is essentially number theory with complex numbers thrown into the mix. The hypothesis states that all non-trivial zeros of the Reimann Zeta function fall on the critical line. What!?? Ok, sorry. That is not very helpful. Lets just say that there is a critical relationship between this function and our understanding of the distribution of prime numbers. And of course prime numbers are the building blocks of all other numbers and insanely important in a number of fields that affect our lives critically – one of which is modern cryptography. So basically all of the encryption algorithms that allow us to make a payment online, log in to our bank account, or maybe even send an encrypted text message depend on the Reimann hypothesis.
In other words, this thing is a pretty big deal – not just in the world of math, but also in the world of technology and beyond. The first thing we need to understand about this animal is that even though it has not been proven by a formal proof, it has been shown to be true for billions of cases. Think of this way – you want to know if it is true that no yellow Honda accords will ever pass by your house at exactly 2 in the morning. That is your hypothesis. So every night for 40 years you check. That would be 14,600 cases. And you never see the yellow Honda accord pass by. From a mathematical perspective you have not proven anything. But you would be pretty safe to make assumptions in your daily life based on this observation. For example you probably would be willing to gamble $100 that this would never happen in your lifetime. Well imagine that you were up for billions of nights (because you have infinite life in this example, bear with me) and you never see the Honda accord. You would be tired AND you would be pretty sure the Accord was not going to pass by. Maybe you live in an enclave with only Ferraris – I don’t know.
So that is where number theorists start when they look at Reimann. They know its true for billions and billions of examples, but they cant rule out that its not true. And NOW to the part about big data.
Professor Andrew Odlyzko at the University of Minnesota is the foremost computational number theorist studying Reimann. In fact if you go to his website, you can download (for FREE!) “The first 2,001,052 zeros of the Riemann zeta function, accurate to within 4*10^(-9)”
In other words, you can see a record of the first 2 million nights where the yellow Honda accord did not show up in front of your house at 2 am. Now this dude is an amazing professor and mathematician and he has used state of the art techniques for decades to explore Reimann and thus the distribution of prime numbers. I don’t know him personally, but I’m willing to make the bet that he has not used Apache Spark yet as a way of finding new zeros of the Zeta function (although I could easily be proven wrong!).
You might ask – How would using Spark be any different that the uber powerful calculations that have already been done to find billions of zeros of the Zeta function? Well, for one, it’s the fastest open source method for performing parallel computations on distributed networks that has ever been invented (thank you Berkley Amp Lab). Second of all, we can run it on an arbitrarily large set of commodity servers in the cloud. Third it runs in-memory so that calculations can be 10 times faster than Hadoop Map Reduce. And finally – it has a Python interpreter Pyspark and we know that Python has awesome mathematical packages, such as scipy that already have built-in functionality, in this case:scipy.special.zeta(x, q) = <ufunc ‘zeta’>
So lets recap: Math nerds of the world are trying to prove or disprove the Reimann Hypothesis. The whole world of cryptography and our modern understanding of the distribution of prime numbers is built on the assumption that this Hypothesis is true. Some really smart people, such as professor Odlyzko have shown this to be true for an insanely large number of test cases. The advent of the Big Data era has produced tools such as Spark that can process pentabytes of data over a massive number of computing clusters in a reliable manner AND we have Python to help us do the math. In other words, we might have a new angle at the greatest unsolved problem in Mathematics. On the other hand, as many computational number theorists have wondered, there might not be a technical way of proving this hypothesis. It might require the invention of some new math in the way that K theory was needed for super string symmetry or the way that modular elliptic curves needed to be invented for Fermat’s last theorem to be proven. But, who knows, it might be worth a try!k
