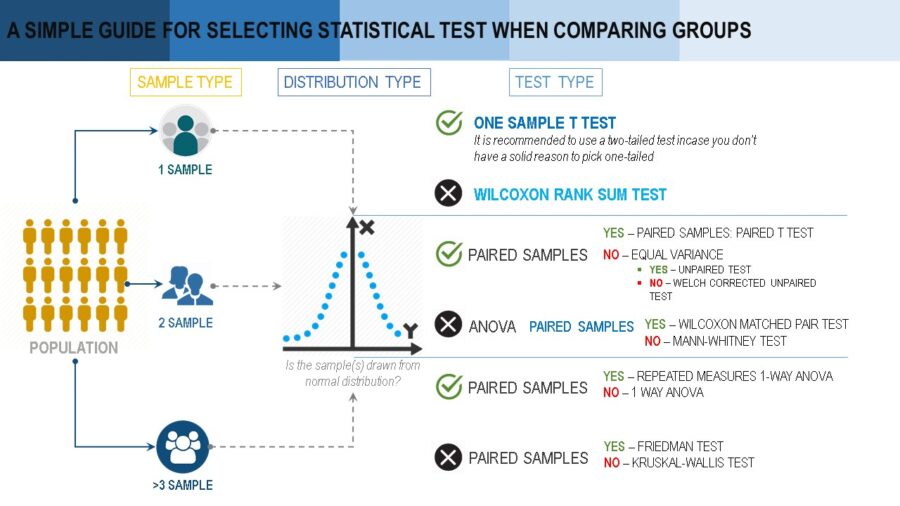
Selecting the right statistical test can prove to be a daunting task for anyone. This infographic presents a step by step approach for the test selection process. This way of looking at various conditions to pick the appropriate tests will allow the audience to visualize and remember the process easily.
However, it is also very important to have the basic understanding of statistics, related terms and concepts. It will not be a wrong statement to make that the correct statistical selection process leads to correct decisions and inferences.