P-Value Explained in One Picture

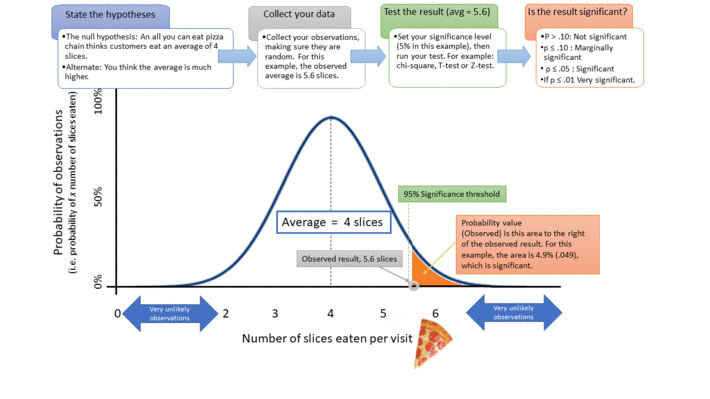
P-values ("Probability values") are one way to test if the result from an experiment is statistically significant. This picture is a visual aid to p-values, using a theoretical experiment for a pizza business.

1 member likes this

Comment

You need to be a member of Data Science Central to add comments!

Join Data Science Central

Comment by Vincent Granville on Friday: I agree with you Stephanie. If you see any of your articles / pictures stolen, let me know. We also monitor plagiarism and illegal copies. I had some of my books stolen and illegally re-published elsewhere (as most authors do) and I took care of it. The good news, the plagiarists get very little traffic, and very bad quality traffic. Thanks Stephanie for the great work!

Comment by Stephanie Glen on Friday: Lance,

If people want to steal, then they'll probably just Photoshop out any credit ;)

Have you checked out this article? Lengthy, but does a good job: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4877414/

Comment by Lance Norskog on October 31, 2019 at 12:14pm: There's so much unaccredited stuff on the net, you know. Maybe sign your stuff, especially when it's this high quality!

Do you know of a good explanation of p-values v.s. power? Especially how both help determine whether to act on the outcome of an experiment?

Comment by Stephanie Glen on October 31, 2019 at 7:46am: Lance, I made this picture.

Comment by John Predmore on October 21, 2019 at 11:10am: My stats professor summed it up succinctly: "p-value is the likelihood, if you reject the null hypothesis, that you would be wrong". In other words, the experiment produced a result due to luck of the draw which led you to conclude the null hypothesis was violated, when in actuality, the null hypothesis was true. If you ran the pizza survey many times, pizza consumption is normally distributed and the true average consumer ate 4 pizzas, over the long run the test result of 5.6 or more would be generated in 4.9% of repeated sampling (everything else being constant). Thus, for many experiments, you want p-value close to zero.

Rejecting the null hypothesis is the outcome most people care about and most statistical experiments are fashioned to produce, because rejecting the null hypothesis is a stronger statistical statement than being unable to refute the null hypothesis due to insufficient evidence.