I’ve recently spent a bit of time getting to grips with Markov Chains. I’ve created a jupyter notebook which attempts to give an “intuition” into the basic concepts; an overview of some of the maths involved and a idea to use “social mobility” probability density functions with Markov Chains to estimate long term “social class” proportions.
This paper has three sections. The first section uses simulation to develop an intuitive understanding of the ideas behind Markov Chains; the second section looks at some of the mathematics used to represent the problem, leading to the standard eigenvector representation and the final section describes an idea to use Markov Chains together with a probability distribution model of social mobility to predict long term “social class” proportions.
- Source code
- Multi State Markov Chains
- Simulation
- Markov Model Based on a Social Mobility Probability Distributions
- Collecting Data
- Example Output Based on Dummy Data
- Plot Predictions Against Data in the BBC Report
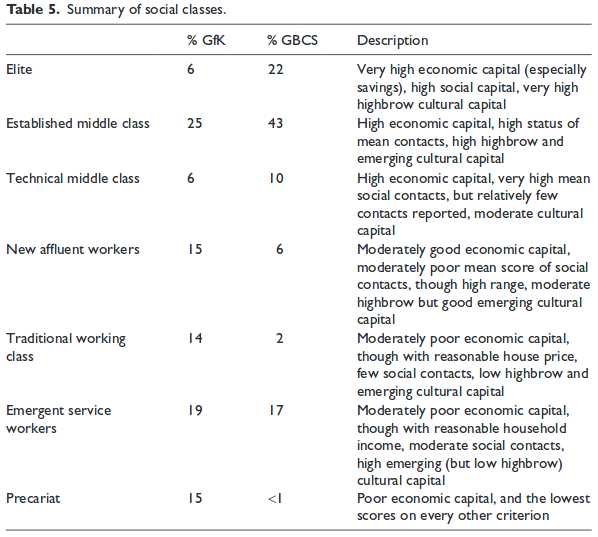
Extract from the article: