The original article is no longer available. Similar (and more comprehensive) material is available below.
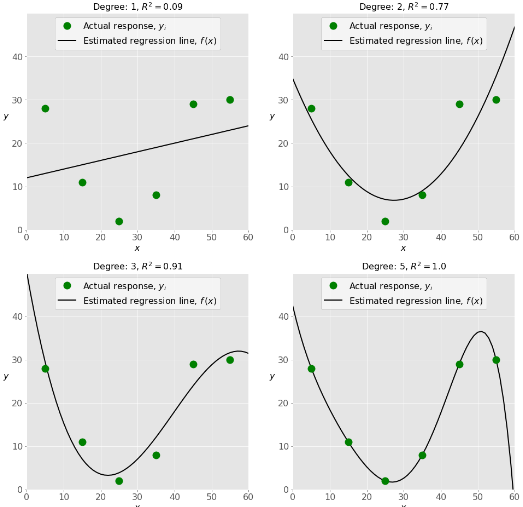
Example of underfitted, well-fitted and overfitted models
Content
Regression
- What Is Regression?
- When Do You Need Regression?
Linear Regression
- Problem Formulation
- Regression Performance
- Simple Linear Regression
- Multiple Linear Regression
- Polynomial Regression
- Underfitting and Overfitting
Implementing Linear Regression in Python
- Python Packages for Linear Regression
- Simple Linear Regression With scikit-learn
- Multiple Linear Regression With scikit-learn
- Polynomial Regression With scikit-learn
- Advanced Linear Regression With statsmodels
Beyond Linear Regression
Conclusion
You can access this material here.
